最小终止距离(MAR)的计算
阅读
2025-09-24更新
最新编辑:想飞的胡萝卜1
阅读:
更新日期:2025-09-24
最新编辑:想飞的胡萝卜1
综述
此文是基于维基百科和从Falcon 4 BMS 4.33 U5版本的遭遇战中提取的TacView数据来完成的。本文旨在清晰阐释最小中止距离的计算方法与概念。需说明的是,本文既非关于超视距机动的实际教程,亦非流体力学课程。未考虑到的场景可能导致实际情况与读者所见存在差异。虽说如此,但是本文所提供的图表和方法力在清晰阐释大功率成功规避导弹的战术的核心要义。所有的案例的想定都是在25000英尺的高度上,但由于战斗场景的动态性,实际高度会相应变化。此外,导弹算法可能使其发射后垂直爬升(译注:高抛发射),并在高空完成大部分巡航阶段(主要涉及AMRAAM和AIM-54),但这恰恰使本分析更具价值——它不仅研究理论情境,更涵盖了“实际”交战案例。
在本文第2版中,我模拟了F-14B的空战场景,新增了AIM-54凤凰式远程主动雷达制导导弹的测试。
在本文第3版中,我使用Heatblur开发的DCS版F-14B重新测试了AIM-54导弹III型,并对凤凰式导弹的三种变体进行了全面验证。
定义
最小终止距离(Minimum Abort Range)是指在与敌机对抗时,飞行员在接敌后仍可转向摆脱其导弹追击的最小距离。该距离能确保飞行员对来袭导弹形成足够的提前量:当导弹飞抵目标位置时,会因为速度衰减过大导致失速坠毁。这种战术被称为利用动能击败导弹,因为此时导弹因动力耗尽只能坠落,无法继续追踪目标。
导弹飞行
超视距导弹的飞行始于发射阶段:点火后发动机启动,导弹开始加速直至发动机熄火(持续6-15秒)。此后由于空气阻力作用,导弹进入减速状态。直线飞行时减速幅度较小,而转弯时过载越大减速越明显。但无论如何,导弹始终处于持续减速状态。这种减速效应的强弱程度,正是决定最小终止距离(MAR)的核心因素。
更有研究价值的是导弹在水平直线飞行状态下的减速(即1G减速状态)——在纯转向脱离(Pure Turn-and-Turn)战术中,实际上飞行员并不需要实施剧烈机动。影响最小终止距离(MAR)的关键因素包括:
- 导弹空气动力学
- 敌机的发射导弹时的速度
- 己方速度
- 高度
导弹飞行动力学
飞行动力学与导弹在无动力飞行状态下的实际减速特性密切相关。不同型号的导弹在相同时间内速度衰减程度不同,因此其最小终止距离也存在差异。事实上,即便使用同一型号导弹,其他变量的变化也会导致完全不同的结果。该因素还直接影响导弹转弯时的减速幅度:某些导弹仅能进行协调转弯,而另一些则可采用失速转弯(侧滑转弯)后重新恢复协调飞行的机动方式。大多数现代红外制导近程导弹采用失速转弯,因为其发动机工作时间通常持续整个飞行阶段(据命中目标只有5-7秒)。
失速转弯通常不属于超视距导弹的标准机动动作,但诸如配备网格舵的R-77导弹(可实现瞬时150度每秒转向)等例外情况确实存在。怎么判定的这是侧滑转弯?因为在马赫2状态下进行协调转弯意味着导弹需要承受161G过载——这显然超出其结构极限。而R-77甚至能达到4马赫的速度!R-77之所以具备这种特性,或许因其红外制导型号(R-77T)需要在飞行末段实施大机动动作。然而失速转弯的问题在于高攻角导致的高阻力。
在任何情况下,导弹飞行动力学影响其阻力和加/减速特性。
敌机速度
导弹发动机熄火时的速度与发射平台的速度密切相关。由于导弹始终处于持续减速状态,更高的熄火时速度会增大最小终止距离(MAR)——因为在导弹有更多的动能。从1.5马赫、4万英尺高度飞行的F-15战机发射AIM-120导弹,与从在海平面以0.7马赫飞行的F-18发射同型导弹,两者的效果截然不同。
简而言之,初始发射速度越高,导弹在无动力飞行阶段的起始速度就越大,最小终止距离(MAR)也随之增大。
己方速度
己方的速度直接影响最小终止距离(MAR):当我方速度增大时,与导弹的相对速度就会降低。例如,若我以700节速度实施脱离,导弹初始追击相对速度为1100节并在持续减速中;但若仅以400节速度逃离,导弹初始追击相对速率将高达1400节。这300节的速率差往往意味着生死之别。
己方飞得越快就能更快逃离导弹,所以有更小的MAR。
高度
高度是一个影响阻力的因素。简化后,一个飞行物的阻力等于
[math]\displaystyle{ \begin{equation} \frac{{C_L}{A_R}{V ^2}\rho}{2} \end{equation} }[/math]
其中,[math]\displaystyle{ \rho }[/math]是周围空气的密度,取决于飞行高度。因此阻力与高度呈反比的。从转向脱离的角度,降低高度更佳,因为更高的阻力和更小的MAR。
AA-x vs AA-x
由此可见,影响最小终止距离(MAR)的因素颇为复杂。即便对于同一型号导弹,因素1相同但其余三个因素的不同的组合也会导致巨大差异:某种情况下MAR可能达到20海里,而另一种情况下可能勉强达到7海里。
另一方面,不同型号的导弹(AIM-120C和AIM-7M)也可以在设置适合的情景下有相同的MAR。
对于攻击者
作为攻击者,你应该想提高MAR。在因素1(导弹空气动力学)相同时,你可以通过以下手段增大MAR:
- 增大发射前速度
- 增大高度
对于防御者
作为防御者,你应该想降低MAR。在因素1(导弹空气动力学)相同时,你可以通过以下手段增大MAR:
- 增大速度
- 降低高度
MAR的确定
最小终止距离(MAR)与导弹的减速特性高度相关。在理论计算中最难确定的是导弹的末端速度,因为这关系到导弹维持飞行高度的能力。导弹的失速速度是多少?需注意在超视距作战高度(>20,000英尺)时,指示空速(IAS——维持机翼升力的速度)与真实空速(TAS——导弹接近目标的速度)存在显著差异。若导弹在0.6马赫时失速,意味着在海平面高度其失速速度约为400kIAS)/400kTAS;但在25,000ft高度时,400kIAS对应的真空速却高达600节。
当然,这些特性与实际导弹空气动力学相关,此处不再深入探讨。只需明确:大弹翼导弹的失速速度小于小弹翼导弹,但代价是因阻力更大而减速更快。在我们的计算模型中,将统一采用400kIAS(相当于25,000ft高度的600节真空速)作为导弹失速速度,并假定所有空战均在此25,000ft发生。有意思的是,我们其实也不用关心导弹的实际失速速度——即便一枚失速速度为600kTAS的导弹,在魔法下仍维持300kTAS飞行,但也可视为已失效。因为目标速度:在转向脱离战术中,若导弹速度低于目标速度,即可判定其失速。因此对于速度低于600kTAS的目标,我们采用600节作为失速速度标准;若目标速度超过600节,则直接以目标速度作为导弹失速判定基准。
案例一:基于最大射程(MOR)的最小逃脱距离(MAR)——匀减速模型
在BVR中最没用的参数就是由生产商或者杂七杂八的网站给出的最大射程。
毋庸置疑,基于该参数计算的最小逃脱距离(MAR)实战价值有限,但作为MAR确定的入门指引,其教学意义却十分重大。
在匀减速模型下计算最大射程(MOR)中的减速过程时,设定场景如下:在发射的瞬间导弹达到最大速度,且导弹对目标尾追(cold)。导弹的运动被视为匀减速直线运动,通过运动方程计算恒定减速值,进而求得导弹达到失速速度前的飞行距离与时间,并减去该时段内目标的移动距离,得到MAR。需特别注意:当目标速度低于600kTAS时,导弹失速速度取600 kTAS;若目标速度更高,则设置的导弹失速速度等于目标速度。
这种计算方法的局限性在于其假定整个导弹飞行过程中的加速度恒定不变。这与现实情况完全相反:导弹速度越快,其加速度的绝对值实际上越大。在后续的案例II中,我们将采用更贴近现实的加速度模型,其中加速度将根据导弹实时速度进行动态推导。
该计算模型的另一项简化在于假定导弹发射后瞬间达到最大速度。而实际情况中,导弹发动机将工作6-10秒,在此期间导弹将持续加速至最大速度(或接近最大速度)。在案例III中,我们将进一步把导弹的加速阶段纳入计算考量。
恒定的加速度可由运动方程求解。
[math]\displaystyle{ \begin{equation} d=d_0+v_0 t + 1/2 a t^2 \end{equation} }[/math]
[math]\displaystyle{ \begin{equation} v=v_0 +a t \end{equation} }[/math]
式中,[math]\displaystyle{ d }[/math] = MOR,[math]\displaystyle{ d_0 }[/math]=0,[math]\displaystyle{ v_0 }[/math]是导弹最大速度,[math]\displaystyle{ v }[/math]是导弹的失速速度。求得
[math]\displaystyle{ \begin{equation} a = \frac{{{v^2}_{STALL}}-{{v^2}_{MAX}}}{2 MOR} \end{equation} }[/math]
[math]\displaystyle{ \begin{equation} t = \frac{2 MOR}{v_{MAX}+v_{STALL}} \end{equation} }[/math]
有了加速度,可以计算导弹减速至实际失速速度时飞行的距离
[math]\displaystyle{ \begin{equation} d_{missile}=v_{MAX} t +1/2 a t^2 \end{equation} }[/math]
式中,[math]\displaystyle{ a }[/math] 由之前计算得到。显而易见,当目标速度小于600kTAS时,该距离就等于MOR。
目标为直线匀速运动,其飞行距离为
[math]\displaystyle{ \begin{equation} d_{target} = v_{target} t \end{equation} }[/math]
t是导弹的飞行时间。MAR由下式给出
[math]\displaystyle{ \begin{equation} MAR=d_{missile}-d_{target} \end{equation} }[/math]
本文将该方法用于几种非常常见的导弹。
本次分析涉及的导弹型号包括:AIM-120C AMRAAM、AIM-120B AMRAAM、AIM-7M"麻雀"、R-27ER/AA-10C"杨树"、R-77/AA-12"蝰蛇"、"马特拉"超530D以及远程导弹AIM-54"凤凰"。各导弹性能参数详见表。本案中不对"凤凰"导弹过多探讨,因其具备最大射程与最小减速特性——若仅以此为标准,它无疑是史上最优异的导弹。但在案例II和III中,相关结论可能出现显著变化。
| 最大速度(kTAS) | MOR(nm) | a(kts/s) | |
|---|---|---|---|
| AIM-120C | 2408 | 60 | -13 |
| AIM-120B | 2408 | 40 | -19 |
| AIM-7M | 2408 | 38 | -20 |
| R-27ER | 2709 | 70 | -14 |
| R-77 | 2408 | 45 | -17 |
| 530D | 2709 | 20 | -48 |
| AIM-54 | 3010 | 100 | -12 |
关于加速度计量单位的说明:本文采用kt/s)而非更常见的m/s2或其他标准单位,此举可能会让部分读者感到不解。本文选择该单位系因其在航空动力学场景中具有最直观的操作实用性。
| MAR(nm) | |||||||
|---|---|---|---|---|---|---|---|
| 目标TAS kts/Mach# |
500/.83 | 602/1 | 722/1.2 | 903/1.5 | 1204/2 | ||
| AIM-120C | 39 | 35 | 30 | 23 | 12 | ||
| AIM-120B | 27 | 24 | 21 | 16 | 8 | ||
| AIM-7M | 25 | 23 | 20 | 15 | 8 | ||
| R-27ER | 48 | 44 | 39 | 31 | 19 | ||
| R-77 | 29 | 27 | 23 | 18 | 9 | ||
| 超级530D | 14 | 13 | 11 | 9 | 7 | ||
| AIM-54 | 73 | 67 | 61 | 51 | 38 | ||
超级530D为啥在这?幻影-2000C在DCS世界里是个大家伙。虽然在制导方式上与"麻雀"导弹类似,且具有更高的初始速度但射程较短,但该导弹在超视距作战领域确实有其独特优势。
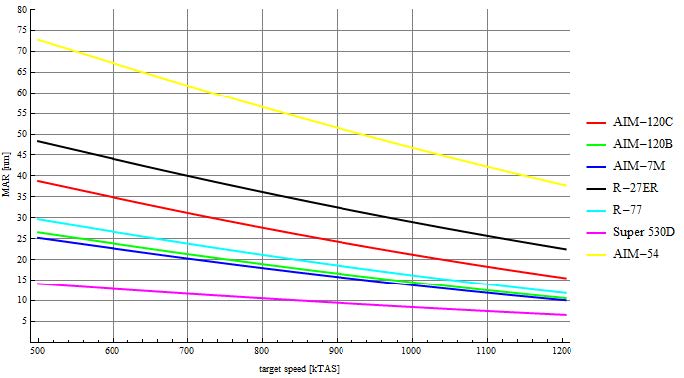
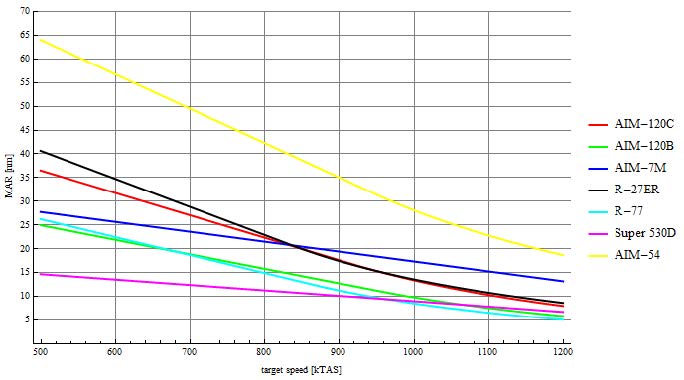
图1给出了基于导弹最大射程(MOR)绘制了不同目标逃逸速度下的最小终止距离(MAR)。从图表可知,R-27导弹凭借其更远的射程和更高的最大速度,成为拦截效能最强的型号。AIM-120C紧随其后,而530D因最大作战半径有限,在保持敌机距离方面表现最差——这在预期之中。AIM-7M位列第二"劣势"导弹,但其性能与R-77十分接近。
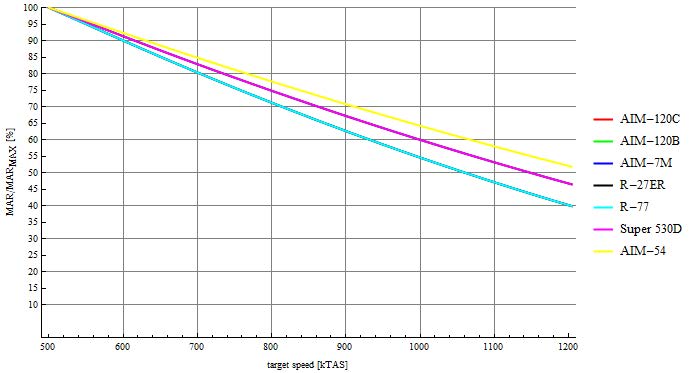
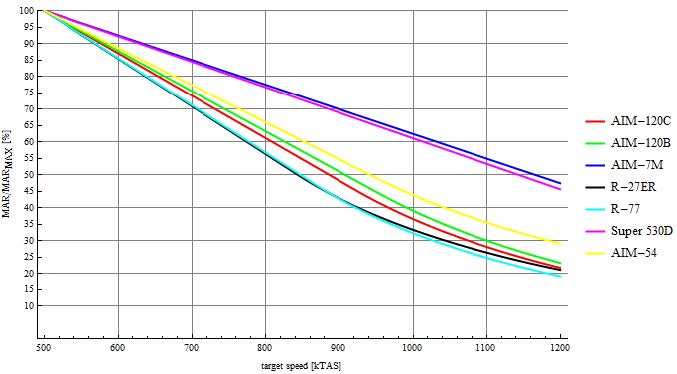
另一个有趣的比较是,导弹提供的最大MAR的百分比与目标速度的函数关系。将最大MAR定义为当目标以500kTAS逃离时计算得出的MAR值。这类比较能够显示在目标实施转向脱离的对抗场景中,导弹动能衰减的速度。下图展示了这项对比结果。
530D看上去没那么糟糕对吧?当目标速度为1150kTAS时,530D依然有50%的最大MAR。同时,R-77只有43%的最大MAR。事实上,在这条青蓝色轨迹线之下,除R-77外还有AIM-120C、AIM-120B、AIM-7M等导弹。即使是AMRAAM-C型导弹,在目标速度提升时保持有效杀伤范围的能力也不及530D与R-27ER。这主要归因于后两款导弹更高的初始速度。在目标速度处于常规区间(700kTAS)时,所有导弹在此项参数上表现相当。
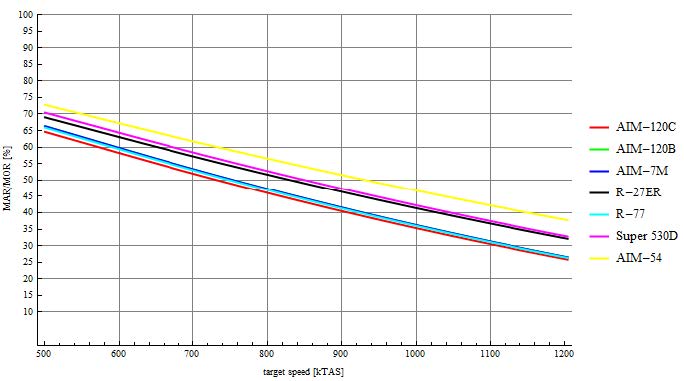
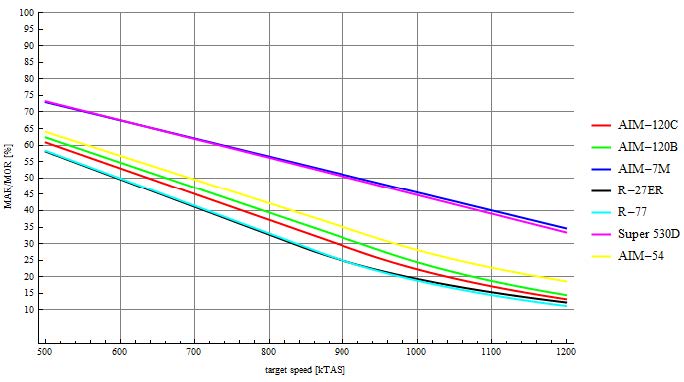
另一个更有趣的是MAR占MOR的比例随目标速度的变化情况。下图给出了比较。最具有威胁的导弹是530D,对于低速目标,530D的MAR占MOR的比例超过70%。当然该导弹的最大射程(MOR)非常小,但值得注意的是,在其整个最大射程范围内,其命中概率远高于其他导弹。
案例二:基于最大射程(MOR)的最小逃脱距离(MAR)——变减速模型
在这个案例中依然采用基于MOR的MAR计算方法,但是加速度在飞行过程中变化。与匀加速模型一样的是MOR的定义:当导弹速度达到[math]\displaystyle{ v_{stall} }[/math]时,导弹的飞行距离是MOR。
本文将导弹飞行过程划分为多个恒定速度段,每个阶段的实际速度取决于前一阶段的速度以及当前导弹速度下的加速度。不过,导弹的加速度为啥会和自身速度相关?虽然这本质上属于流体动力学问题,但仍可从纯运动学角度给出经过推演的答案。阻力的一个简单表达式为[math]\displaystyle{ \frac{1}{2} \rho A C_d v^2 }[/math],式中阻力与速度的平方呈正比。因此,这个在最高速度时阻力值为TacView中实测所得,而在失速速度时减速度为零的条件下根据速度的平方计算加速度。此时自然而然想到的便是比例法则的变体公式:
[math]\displaystyle{ \begin{equation} a= a_{max} \frac{(v_{missile}-v_{stall})^2}{(v_{max}-v_{stall})^2} \end{equation} }[/math]
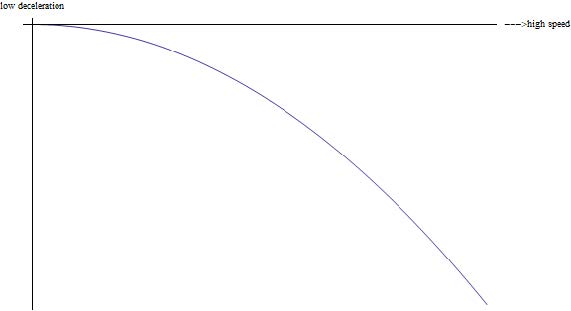
在此案例中[math]\displaystyle{ v_{stall} }[/math]总是等于600kTAS,因为减速特性不与目标速度相关。为直观展现,下图中绘制了加速度-速度曲线。需要注意的是,由于加速度值为负数,图中顶部表示较低减速度,而曲线向下弯曲代表加速度绝对值逐步增大。
方法其实非常简单:计算导弹在变量减速下的飞行距离,再减去目标在相同时间内移动的距离。为此我编写了一个小程序,它根据导弹的最大操作速度、初始减速值、MOR以及目标速度来计算所有参数。
Missile Breakdown
此案例中的运动学参数如表3所述:
| [math]\displaystyle{ v_{MAX} }[/math][kTAS] | MOR[nm] | [math]\displaystyle{ a_{MAX} }[/math][math]\displaystyle{ [\frac{kts}{s}] }[/math] | |
|---|---|---|---|
| AIM-120C | 2`408 | 60 | -49 |
| AIM-120B | 2`408 | 40 | -68 |
| AIM-7M | 2`408 | 38 | -27 |
| R-27ER | 2`709 | 70 | -77 |
| R-77 | 2`408 | 45 | -77 |
| 530D | 2`709 | 20 | -95 |
| AIM-54 | 3010 | 100 | -55 |
在表4中,我加入了一些在案例2的场景中计算的MAR。有些导弹更容易击中目标,而另外一些性能不行。AIM-54由于大幅减速,它的MAR距离也受很大的影响。但是,AIM-54仍然可以达到MOR距离,不用为它惋惜。在案例3中将展示一次“实际”交战的例子。
| MAR(nm) | |||||||
|---|---|---|---|---|---|---|---|
| 目标TAS kts/Mach# |
AIM-120C | AIM-120B | AIM-7M | R-27ER | R-77 | 超级530D | AIM-54 |
| 500/.83 | 36 | 25 | 28 | 41 | 26 | 15 | 64 |
| 602/1 | 32 | 22 | 26 | 35 | 22 | 14 | 57 |
| 722/1.2 | 26 | 18 | 23 | 28 | 18 | 12 | 48 |
| 903/1.5 | 17 | 13 | 19 | 17 | 11 | 10 | 35 |
| 1204/2 | 8 | 6 | 13 | 9 | 5 | 7 | 19 |
比较
下图展示了上文所述的变加速度场景下的导弹最小终止距离(MAR)对目标速度的关系。图中可以看出,R-27ER和AIM-120C导弹的“发射后不管”能力最为突出。但关于AIM-7导弹却有一个意外发现:当目标速度极高(>840kTAS,即1.4马赫)时,由于麻雀导弹的阻力系数较小,它反而成为攻击脱离目标的更优选择。例如针对1100节速度的目标,麻雀导弹的命中距离可达近15海里,而AMRAAM或AA-10E导弹仅能达到10海里。530D因初始阻力过大且最大射程较短而表现垫底。但需要说明的是,当目标速度极高(>1100kTAS)时,530D反而性能超越AMRAAM-B和AA-12导弹。
与最大射程(MOR)匀减速模型下的对比类似,本文分析了图6所示的(MAR)占最大MAR的曲线。在整个目标速度范围内,MAR保持能力最强的导弹是AIM-7M"麻雀"与Super-530D——这两款恰好也是最大射程最小的导弹,且均采用半主动雷达制导。尽管如此,它们的MAR仍出现了超过50%的衰减。而其他型号导弹的MAR衰减率更是高达80%左右。 通过最大作战半径比率图表(图7)可得出其他重要结论:在常规超视距空战速度范围内,"麻雀"导弹与530D导弹能保持超过60%的最大作战半径作为最小逃脱距离。这一表现令人印象深刻,因为其他更先进的导弹仅能维持不足50%的比率。当目标速度极高时,小射程导弹与先进导弹的差距会扩大至20%——后者仅能达到最大作战半径的15%。有人可能认为这是正常的,因为绝对作战半径的差异可以弥补这些百分比差距,但60海里的15%(=9海里,AIM-120C)实际上小于38海里的35%(=13海里,AIM-7M)。
通过MAR占最大作战半径的比例图表(图7)可得出其他有意思的结论:在常规超视距空战目标速度的范围内,"麻雀"导弹与530D导弹的MAR超过60%的MOR。这一表现令人印象深刻,因为其他更先进的导弹仅有不足50%。当目标速度极高时,小射程导弹与先进导弹的差距会扩大至20%——后者仅能达到15%MOR。有人可能认为这是正常的,因为绝对MOR的差异可以弥补这些占比差距,但60海里的15%(=9海里,AIM-120C)实际上小于38海里的35%(=13海里,AIM-7M)。
需要明确的是,上述分析并非认定"麻雀"或530D是最佳导弹——事实远非如此!导弹的实际作战效能高度依赖于运用方式。R-27ER导弹确实能在70海里距离(基于最大射程)发射,从而迫使敌机在开火前转入防御姿态,这本身就是巨大优势。反之,配备20海里最大射程的530D导弹的"幻影-2000C"战机,必须在超视距空战中采取极致待机博弈与防御战术才能保持竞争力,因为极可能遭遇对方的先手打击。但反过来说,若以900kTAS(1.5马赫)的高速面对AMRAAM-C导弹,转向脱离战术将有效抵消敌机的射程优势,至少在先手攻击层面实现战术均势。
案例三:基于TacView分析的MAR计算
这是个更真实的场景。在进行超视距空战训练时,作者大量运用TacView战术分析系统复盘空战过程,分析战术决策的得失。通过可视化交战回放,能够在一定程度上测定多项参数。与之前仅需测定导弹无动力飞行减速情况的方法不同,本次将针对转向脱离战术场景,逐秒追踪导弹直至失速的全程速度变化。
通过获取导弹的逐秒速度数据,可支持加速度的精确分析,从而得出更贴近实际的导弹有效射程。该方法与前两种方式的共性在于都需要计算导弹飞行距离与目标移动距离的差值。但本次实际掌握了导弹的速度变化曲线,本质上是在运用更真实的减速特性模型,因此有望实现更精准的最小终止距离(MAR)计算。或许这种方法最大的优势在于:其计算结果完全摆脱了对最大作战半径(MOR)的依赖。
Missile Breakdowm
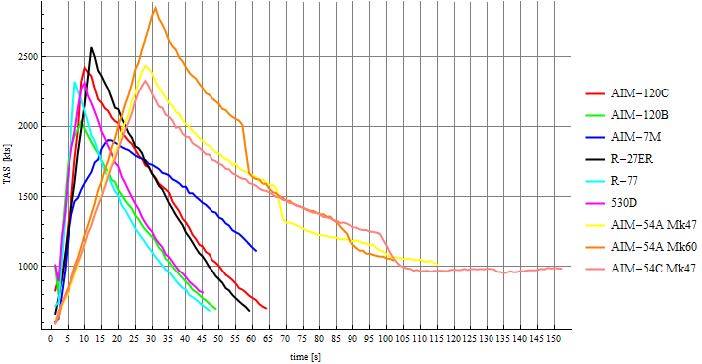
正如前文所述,我掌握的"唯一"导弹数据是其飞行全程的速度-时间序列。但由于这些数据采集自真实交战环境下的“实际”遭遇战,应能得出更具实用价值的结果。图8将六款导弹的速度演化曲线整合于同一图表,以便直观对比各导弹在实际飞行中的动力学特性。
一个有趣的现象是:AIM-7M"麻雀"导弹呈现出两级火箭发动机的加速特征。这完全符合实际情况——该导弹搭载的赫克里斯MK58双脉冲固体火箭发动机采用两种燃烧速率不同的推进剂。初始阶段两种推进剂共同产生高推力,当速燃推进剂耗尽后,导弹仅依赖缓燃推进剂工作,加速度随之下降,这与图表曲线完全吻合。这个细节充分证明模拟器开发者提供了卓越的飞行动力学模型Wow!
通过图表还可观察到:导弹并未完全达到理论最大速度(2408/2709/3010knot),实际值往往偏低或偏高(如图中R-27ER达到2571kTAS,而"凤凰"导弹仅达2012kTAS)。这是因为作者在任务中尝试还原交战时的真实气象条件,大多数情况下并非国际标准大气(ISA)。另一重要因素是:实际交战中我方通常处于对敌机高速迎头状态,当敌方发射导弹后,我方需立即转向脱离。这种规避动作会迫使导弹同步转向,从而损耗部分初始速度。急转弯带来的速度损失最小,但会对导弹施加过载压力,人类飞行员多数情况下采用浅转弯(<4G),而人工智能则常实施急转弯(>7G)。图9展示了两种不同脱离转向对追击导弹的影响差异。
另一个值得注意的现象是部分导弹采用"高抛"弹道:发射后凭借火箭发动机助推迅速爬升,通过增加高度来降低阻力、延伸射程。这种战术的典型代表是AMRAAM与"凤凰"导弹。AMRAAM针对位于25000英尺高度的目标会爬升5000-10000英尺,而"凤凰"导弹为攻击位于30000英尺目标曾跃升至42000英尺高度——这导致其最大真空速(马赫5)仅能达到约2800节。这种弹道差异正是导致数据偏差的主要来源。但在虚拟空域中,没有理智的飞行员会放任敌机获取任何优势,何必为了追求导弹理论极限射程而偏离真实交战环境呢?本案例所呈现的正是最真实的交战!
可以看出并非所有导弹最终都能达到600节的速度。这同样是由于测量数据源自"真实"场景所致。这些导弹比理论模型中更早出现失速,且失速速度各不相同——这一点非常宝贵,因为它让我们能够清晰区分各导弹的实际性能,而这正是在理论模型(所有导弹都在相同速度下失速)中无法获得的重要特性。
但分析图8能获得其他贴近现实的参数。例如不同导弹的发动机燃烧时长:我们可以看到R-27ER的燃烧时间约为12秒,这与实际数据完全吻合!AIM-120C和B型导弹的燃烧时间显示为10秒,在最后1秒加速度出现下降,因此实际燃烧时间更接近7-9秒。这个数据与AMRAAM导弹的真实性能记录是一致的。
还需注意的是,加速度最大的导弹是被称为"AMRAAM斯基"的R-77导弹,但其减速幅度也较高。作为主动雷达制导导弹,它专为高机动性目标设计,在不可逃逸区内基本无法规避——因其能实现150度/秒的转弯率。但若在不可逃逸区外发射,则无异于浪费弹药。
减速幅度最小且燃烧时间最长(约16秒)的是麻雀-M导弹。该导弹自1982年服役以来,堪称专为拦截任务而生。其在追击高空高速飞行的战术轰炸机时,速度衰减微乎其微。
接下来我们将通过"真实"交战场景的计算数据,观察不同目标速度条件下不可逃逸区的数值表现。
| MAR(nm) | |||||||
|---|---|---|---|---|---|---|---|
| 目标TAS kts/Mach# |
500/.83 | 602/1 | 722/1.2 | 903/1.5 | 1204/2 | ||
| AIM-120C | 17 | 15 | 13 | 10 | 6 | ||
| AIM-120B | 11 | 10 | 8 | 6 | 3 | ||
| AIM-7M | 25 | 23 | 20 | 15 | 8 | ||
| R-27ER | 16 | 14 | 12 | 10 | 6 | ||
| R-77 | 10 | 9 | 8 | 6 | 3 | ||
| 超级530D | 12 | 11 | 9 | 7 | 4 | ||
| AIM-54 | 32/34/36 | 28/31/32 | 25/28/27 | 19/23/19 | 9/14/6 | ||
表5给出了TacView实战场景下计算得到的MAR。
AIM-54“不死鸟”导弹是迄今为止真正的BVR武器,其最大终止距离可达36海里。这一性能正在预料之中,因为这本就是该型导弹名副其实的设计标准。
在此方案下,各类导弹的射程均在缩小。AIM-120C、AIM-7M与R-27ER对低速目标的打击距离接近18海里,即便针对1马赫的目标仍能保持超视距作战能力;而其余导弹对低速目标射程勉强达到12海里,对抗高速目标时则沦为视距内武器。在MAR上各类导弹的差异并不悬殊,且需注意每位飞行员对导弹告警的规避反应各不相同,这将导致实际射程浮动。例如,以700kTAS飞行的飞行员在收到告警5秒后实施转向,导弹的MAR将增加约1海里。需要注意的是,小坡度会缩减导弹的MAR,而向高密度空域(垂直下降)转向同样的效果。
比较
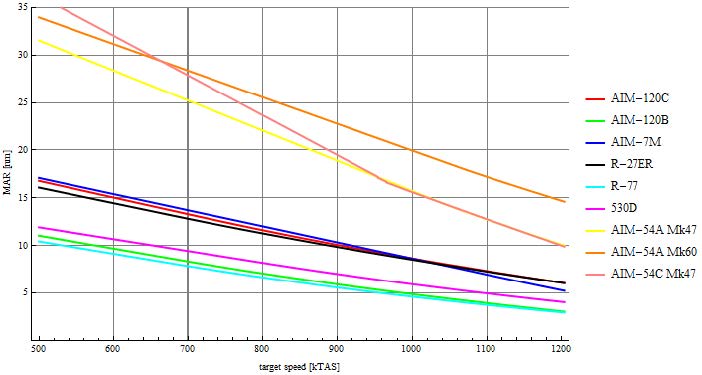
图10呈现了基于TacView实战场景的最小逃脱距离(MAR)与目标速度的关联曲线。在此案例中,拦截效能最强的三款导弹为AIM-120C、AIM-7M"麻雀"和R-27ER——它们在500-700kTAS区间内均能维持12海里的杀伤区。当目标速度超过1000kTAS时,AIM-120C与R-27ER相对"麻雀"导弹的优势进一步扩大。
令人意外的是,超级530D导弹在MAR排名中位列第四。针对低速目标时其MAR可达12海里,即便目标以700kTAS逃离,仍能保持9-10海里的MAR。更值得注意的是,当目标速度进入超音速区间后,超级530DMAR曲线斜率依然平缓——这意味着以1100节kTAS的目标在进入"幻影"战机5海里范围内,必须施展极其复杂的战术机动才能摆脱威胁。
图中可知,AIM-120B与R-77是当前拦截效能最低的导弹。但作为高机动性的"发射后不管"导弹,这一结果并不意外:若目标处于MAR范围内,目标仅凭机动动作几乎无法摆脱追击。
AIM-54A Mk60在保持最大MAR上较好,但AIM47C Mk47的MAR衰减程度则处于其他导弹的范围之内。
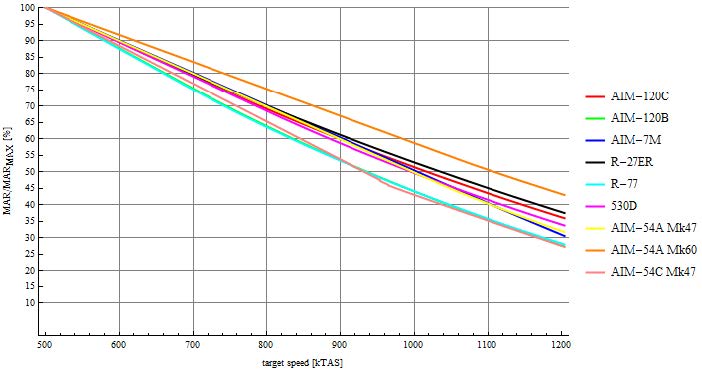
图11展示了不同导弹在目标速度下的最小逃脱距离(MAR)衰减情况对比。在常规超视距空战条件下(目标速度≤700kTAS),多数导弹的MAR衰减约为20%,而R-77与AIM-120B的衰减达到25%。这实际上拉平了各导弹在初始速度、发动机燃烧时间和减速率方面的先天差异。值得注意的是,"凤凰"Mk60针对700节目标仅出现15%的衰减。
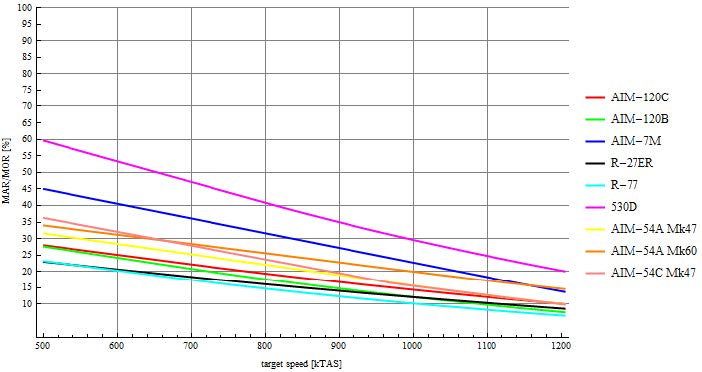
下一张图,图12给出了不同目标速度下向MOR归一化后的MAR衰减比较。
作为最大射程(MOR)最小的导弹,530D在针对低速目标时,即使在25000英尺高度且未达到最大速度,其有效杀伤半径仍能维持超过MOR的60%。即便追击2马赫高速目标,其MAR仍在20%MOR以上(即超过4海里)!
MAR/MOR表现次优的是"麻雀"导弹。虽然其MOR值位列倒数第二,但衰减曲线比530D更为平缓(斜率更低)。
其余四款导弹在全目标速度段中MAR/MOR衰减均低于4%,但实际有效射程与MOR的比值最小。这些导弹高MOR加上最平缓的MAR衰减斜率使得战术威胁性远胜530D或"麻雀"。
AIM-54"凤凰"导弹在保持MAR/MOR比例方面表现最差。其标称射程形同虚设——起始即衰减至84%的MOR,最后MAR占不足MOR比例不足5%。
总结
BVR的第一要义是不要进入缠斗!在敌机越来越近时,MAR距离可以视为交战双方的中线。但是经过多次的战斗,发现MAR其实是个动态的数值。本文的分析试图说明:导弹往往在对手毫无准备时致命,因为导弹的效能曲线在很大程度上被“拉平”了。
确实,你可以在极远距离发射 AMRAAM-C 或 R-27ER 之类的导弹,把敌人逼成防守态势;但那只也意味着对方可能暂时转向逃离几秒钟,之后掉头重新转向你,在距离缩短后向你发射导弹。在 BVR 中把胜负概率拉平是第二要义。如果你在过程中还能让敌人损失一枚导弹,那就更好了。



 沪公网安备 31011002002714 号
沪公网安备 31011002002714 号