气动模型第三部分：空气动力学模块

MediaWiki:Testtoc.js

页面需要校对，可能会出现部分内容难以理解或是出错的情况

×

本文翻译自 https://www.falcon-bms.com/articles/flight-model/the-aero-module/

×

纳维-斯托克斯方程，欧拉方程，还是表格数据？

当我们讨论对空气动力学中的力和扭矩进行建模时，基本上有三种主要选择：

• 第一种是使用纳维-斯托克斯方程和湍流方程，用来计算模型周围的三维气流，并对模型上的压力进行积分。此方法是专业人士对真实飞机进行建模时的做法。遗憾的是，我们的CPU性能不够强大，无法对此进行实时计算。因此基于个人电脑的模拟器不可能采用此方案。
• 第二种方案是对飞机进行简化计算，我认为X-Plane就是采用的此方案。此建模非常有吸引力，因为它与飞机的几何形状直接相关联，这代表着通过定义全局几何参数，建模便会对此输出对应的动作。虽然此方案也很有吸引力，但我认为此模型不够精确，特别是对于F-16来说。实际上，该模型在高攻角和超音速区间的表现非常糟糕，与高保真飞行模型 (HFFM) 数据相比，这显然是一种退步。
• 最后一个方案是使用表格数据，这些数据代表了用于描述飞机性能的所有非尺寸系数。我选择这一方案的主要原因是：
  • 基于现实F-16性能的逆向工作已经完成（HFFM）
  • F-16 已有详尽的风洞试验结果

空气动力学模块的开发

当我开始开发新的气动模型引擎时，主要的想法是使用非电传机（Non Fly-By-Wire，NFBW）来验证物理引擎。在完成验证后，就开始着手实现NASA在兰利开发的F-16模拟器（我最初不打算使用非稳定的飞机来验证物理引擎）。

NASA的技术论文基于F-16的风洞测试，并基于气流作用力的“全局计算”。这为三轴物体系统（译注：yaw/pitch/roll）上的全局力（静态与动态）。

虽然这种力/力矩矩阵表示法（我们称之为“Torsor”）是航空工业/实验室普遍使用的一种表示法，但我发现用它来开发一个全新的物理模型并不方便，因此我决定为NFBW飞行模块选择一种对航空力和力矩更为物理的描述，我称之为“局部计算”（Local Computation）

局部计算 - 非电传机的气动代码

我认为，就物理建模而言，此建模方式是最直观的。它包括为飞机的每个局部表面（右翼、左翼、右升降舵、左升降舵、机身、后缘襟翼（TEF）、前缘襟翼（LEF）等）创建表格数据。

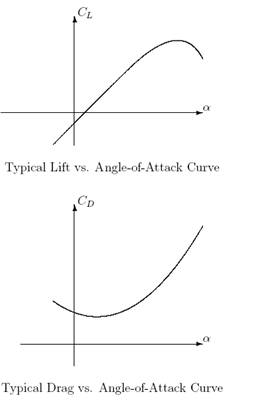
表格数据将包含飞机每个表面的升力和阻力与攻角和马赫的关系。

因此，我们的想法是在飞机运动过程中计算每个表面的局部速度和 AOA，从而得出局部力和扭矩。然后将来自所有表面的力和力矩相加，就得到了施加在飞机上的全局力和力矩。

此空气动力学模块有以下特点：

• 主翼
• 升降舵：经典（固定部件 + 后缘襟翼）或整体
• 方向舵：经典（固定部件 + 后缘襟翼）或整体
• 鸭翼：经典（固定部件 + 后缘襟翼）或整体
• 机身

此外，还开发了一些特殊效果：

• 机身遮蔽（Fuselage Shadowing）
• 尾翼遮蔽（Tail Shadowing）
• 上反效应（Dihedral effect）

我将不详细讨论稳定性问题和飞机运动对每个表面的影响，因为这不是本文的目的。我选择简单地说明一些典型的空气动力/稳定性问题，以让大家了解新的NFBW航空代码的复杂性。

滚转稳定性与转向

自然滚转稳定性

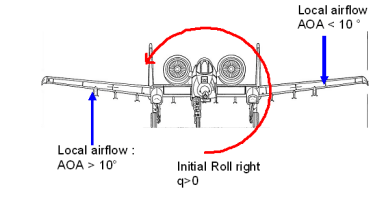
让我们设想一个情况：飞机在以10度攻角直线飞行时，飞行员开始操作操纵杆让飞机向右滚转。那么机体的每个部分都发生了什么？

右翼接收来自下方的部分空气，左翼接收来自上方的部分空气。因此，右翼的攻角大于10度，而左翼的攻角小于10度。这意味着在滚转的过程中，右翼产生的升力要比左翼大的多。

其直接结果是：两侧机翼（主翼）抵消了初始滚转：

• 由于这种自然的反作用力的效果，古董机（无电传）在滚转时通常很稳定。
• 滚转率同样也会受到此效果的限制。

现在便不难理解为什么滚转的时候会引发自旋失速。实际上，如果滚转速度过快，右侧机翼的攻角便会变的非常大，从而进入失速状态。如果右翼失速，则会发生以下两个情况：

• 对滚转的自然反作用力消失，飞机的滚转率增加。
• 失速侧的机翼阻力变的巨大，产生偏航力矩 -- 飞机可能会进入自旋失速。

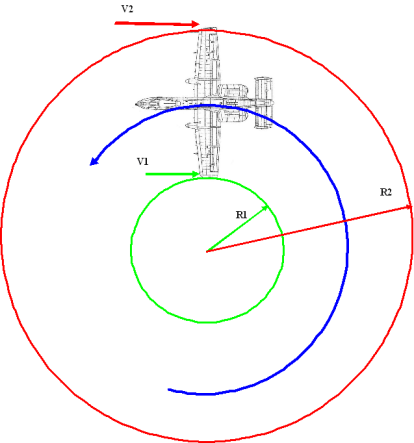
转向时的滚转耦合

R2 > R1 => V2 > V1 => 右翼升力大于左翼 => 向左滚转

在转向时，如果其他的相互作用效果不存在（如：没有侧滑），飞机会有自然性的增加其自身的滚转角度(bank angle)的倾向。为了抵消此效果，飞行员必须在飞机转向时保持一定强度的压杆。

偏航稳定性

尾翼

对于一般的古董机外形来说，尾翼是唯一的垂直面，因此尾翼对飞机偏航稳定性起着至关重要的作用。

当飞机偏航时，比方说向左偏航，此时尾翼会受到来自右侧的气流，因此会产生向左的侧向升力。此时，尾翼会自然的抵消偏航。但是，由于尾翼是古董机上唯一会对偏航产生影响的部件，因此在偏航时尾翼会出现震荡（小幅度的抵消作用）。

• 如果尾翼太小，则其作用便不足以抵消偏航
• 如果尾翼太大，则响应会过于僵硬，尾翼将会陷入震荡状态，最终可能导致另一种类型的不稳定。

因此，为飞机设计一个通吃所有飞行状态的尾翼是非常困难的；有时，工程师会在飞机机腹处增加垂直面，如F-14、MIG-23（甚至是我们的F-16），以增加一些方向稳定性。偏航稳定增强系统（（Yaw Stability Augmentation System）是一种主动式的尾舵控制设备，它可减少震荡并增强偏航控制，它是解决尾翼问题的最终方案。(偏航稳定增强系统也在BMS 中实现，在后续的开发人员说明中将详细介绍）。

尾舵(Rudder)

尾舵的效果取决于多个参数，且受飞机形状的影响，其效果差异也很大。

让我们来分析下不同的效应。我们假设飞行员踩舵向右，此时尾舵自然也转向右侧。

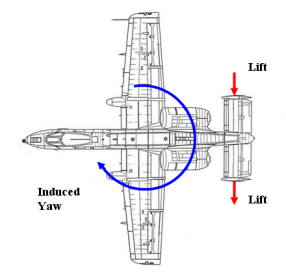
• 作为主要的效应，转向右侧的尾舵会产生一个向左的升力；因此，由于该力的作用点位于尾翼的气动中心，这将产生一个向左的 X 扭矩。此时飞机的初始反馈是向左滚转

• 同时，左侧升力会产生向右的偏航，机头将会指向右侧。

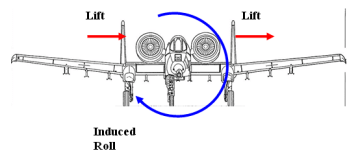
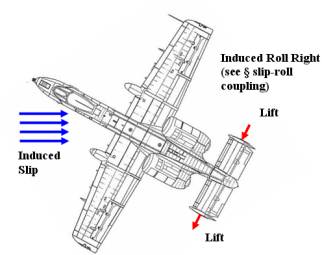
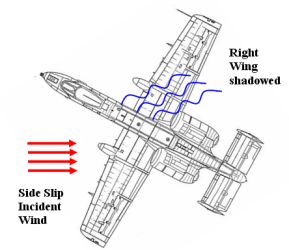
• 作为次要效应，向右的偏航会导致机身向左的侧滑，倾角效应和机身遮蔽通常会导致向右的滚转（见下图）。

有时，尾舵产生的滚转效应非常重要，以至于飞行员会只使用尾舵进行滚转。高速飞行中的F-14就是这样。实际上，后掠翼的角度非常重要（类似于上反效应(dihedral effect)），任何来自尾舵输入所导致侧滑都会引发巨大的滚转......这种动作被称为 “尾舵滚转”（Rudder Roll）。

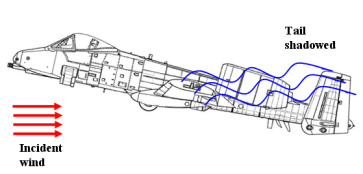
尾翼遮蔽(Tail Shadowing)

当飞机的攻角变的很大且气流不再是层流时，就会造成尾翼处于从主翼而来的干扰气流中的情况。这会降低尾翼的效率，影响偏航稳定性。

侧滑 - 滚转耦合

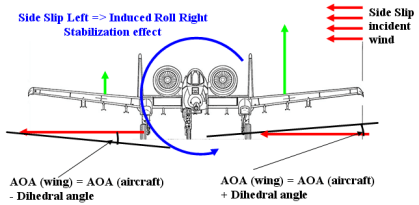
上反效应经常被用于提升飞机的滚转稳定性。

左翼升力 > 右翼升力

在上面的场景中，如果飞机进入侧滑 - 假如说是向左侧滑，那么上反效应所导致的结果是，左翼的攻角显著大于右翼（也就是左翼升力大于右翼）。最终结果就是飞机向右滚转。

在转向时，飞机的自然趋势是向转向侧滑动（由于重力），之后，上反效应将导致飞机向转向的反方向滚转，因此飞机会自然恢复到直线飞行。

因此，上反效应是飞机的自然滚转稳定帮手。需要注意的是，后掠翼角度的效果与上反效应类似（角度越大，效果越明显）。

上反效应在侧滑和滚转之间产生了自然的耦合效果。

机身遮蔽

当飞机的侧滑角很大时，机身会严重的干扰机翼下侧的气流。

右翼所受到的空气比左侧的少。这就导致在上面的场景中产生了不对称升力；飞机进入向右滚转的状态。此现象有时会非常严重，甚至会导致机翼失速 - 自旋失速。

非电传机模型的总结

所有这些效应（并非这里所描述的全部效应）都同时在现实世界中发生作用。有时一种效应会抵消另一种效应，有时则不会。

然而，这一切的意义并不在于单独识别每一种 “效果”，而是在于将所有这些物理效果混合在一起，让模拟机感觉就像真的一样。

总之，我对面向原因而不是面向结果的编程路线的效果非常满意。其结果正是我所期待的 - 将Falcon 4.0的飞行体验提高到了一个新档次。

全局计算 - F-16的空气动力学编程

为BMS（AFM）开发的F-16气动模型的核心主要基于1979年在兰利开发的NASA模拟机

资料来源见 NASA 资源中心（或点击下方)：

NASA技术文件1538(TP 1538)“Simulator Study of Stall / Post Sall Characteristics of a Fighter Airplane with Relaxed Longitudinal Static Stability”

空气动力学数据

NASA模拟中使用的气动数据来自于NASA埃姆斯和兰利研究中心的风洞设施中对F-16的次比例模型进行的低速机翼静态和动态（力振荡）风洞试验。

对模型的描述由6个“全局”气动系数所组成：

力：

• CL：升力系数（参考气流）
• CD：阻力系数（参考气流）
• CY：Y轴力系数（参考机体）

力矩：

• Cm：俯仰力矩
• Cn：偏航力矩
• Cl：滚转力矩

NASA对F16模型进行了风洞试验，在最大可能的条件下（静态和动态）评估了所有这些参数。然而，这些测试都是在相当于 0.6 马赫的条件下进行的 - 这对于我们所设计的，专门在整个飞行包线内飞行的气动模型是完全不够的。

值得庆幸的是，HFFM的数据是根据实际性能图表进行重新设计的，这意味着HFFM数据包含了整个飞行包线（0马赫到2.2马赫）的CL和CD。

关于力矩系数，除了0.6马赫的风洞试验外，找不到其他更多的数据了。不过，由于FLCS的功劳，在整个飞行包线内，俯仰/滚转/偏航行为都得到了人为的完全控制。因此我们可以说，在整个飞行包线内套用0.6马赫的力矩系数都不会导致气动模型与实际偏差太多。实际上，从0马赫到0.6马赫，力矩系数的变化并不大，而在0.9马赫以上时，气动模型显然是在一个非常低的攻角包线上变化的，因此模型的俯仰/滚转/偏航反应主要受FLCS的控制，而非纯空气动力学系数。

最后，我们打算使用：

• HFFM关于CL/CD（和推力）的数据
• 采用NASA数据用于其他系数

HFFM 和 NASA 数据的结合无疑确保了F-16在整个飞行包线内的高仿真精度。

空气动力学数据的依赖关系

在本文中写下所有关于不同系数与参数间的关系方程是没有意义的。不过，为了让你对模型中的动力和耦合有所了解，下面的图表总结了这些依赖关系。NASA技术文件中的所有数据都已包含在AFM中，因此AFM包含了所有这些依赖关系；它代表了数千个系数。这里的所有这些依赖关系会让人感觉 “轨道上的飞机 ”就像一场古老而可怕的噩梦。

变量列表：

• [math]\displaystyle{ \alpha }[/math] = 攻角
• [math]\displaystyle{ \beta }[/math] = 侧滑角
• [math]\displaystyle{ p }[/math] = 滚转率
• [math]\displaystyle{ q }[/math] = 俯仰角
• [math]\displaystyle{ r }[/math] = 偏航率
• [math]\displaystyle{ \delta sb }[/math] = 减速板偏转
• [math]\displaystyle{ \delta lef }[/math] = 前缘襟翼偏转
• [math]\displaystyle{ \delta h }[/math] = 升降舵偏转
• [math]\displaystyle{ \delta r }[/math] = 舵偏转
• [math]\displaystyle{ \delta a }[/math] = 副翼偏转
• [math]\displaystyle{ ds }[/math] = 深度失速

空气动力学系数	变量依赖
CL/CD	从逆向工程得来
CY	[math]\displaystyle{ \alpha,\beta,r,p,\delta a,\delta lef,\delta r }[/math]
Cm	[math]\displaystyle{ \alpha,\beta,q,\delta h,\delta lef,\delta sb,ds }[/math]
Cl	[math]\displaystyle{ \alpha,\beta,r,p,\delta h,\delta a,\delta r,\delta lef }[/math]
Cn	[math]\displaystyle{ \alpha,\beta,r,p,\delta h,\delta a,\delta r,\delta lef }[/math]

特别感谢所有参与费力复制这些系数的 BMS 成员。