BMS AIM-120索敌机制探讨
阅读
2026-01-16更新
最新编辑:glamcurrent
阅读:
更新日期:2026-01-16
最新编辑:glamcurrent
简介
自 Falcon 4.0 发布以来,尽管 HPRF 和 MPRF 目标获取模型的概念多年来得到了改进,但 AIM120 目标获取模型仍然非常简单。
原版游戏中的目标捕获模型有个很大的问题:在AIM-120已经处在HPRF和MPRF搜索阶段时,在发射导弹时机载雷达(FCR)所选择的目标会自动传输给导弹导引头。如果在数据链引导阶段结束时目标位于导引头视场内(并且具有 HPRF 的正闭合速度),则导引头将自动捕获目标,然后对导弹进行自主引导。因此,你能意识到原版中的120弹载雷达捕获模型除了会对雷达视场(FOV)进行相关计算以外,完全不会考虑距离/信噪比和雷达相关的其他计算步骤。这也代表你在机载雷达上瞄谁那导弹就毫无偏差对谁追踪。
在经过多轮测试和改进后,我们已经将这个超-简单的建模改进成至少在游戏性上能接受和有趣些。首轮的模型更改已经在4.37.0中呈现,其中包含有成吨的错误和不一致,这也将在未来的补丁和新的迭代中修复。
目标引导阶段
从[1]中我们可以得到,120可以使用4种模式来发射(至少在F/A-18)中:
- 首选发射模式是惯性指令(Command Inertial)模式,其中导弹通过使用射频数据链接收来自飞机的瞄准指令,该数据链每 0.5 到 1 秒提供一次更新,具体取决于飞机雷达的发射模式。
- 惯性主动(Inertial Active)模式是一种完全的射后不理模式,AMRAAM将会主动引导到发射前已经确定的某个惯导点,飞机将不会在发射后更新任何导弹导航信息
- 导弹也可以在受到电磁干扰的环境中进行干扰源追踪(home on jam)(HOJ)模式发射引导
- 当没有雷达瞄准时,导弹也可以以视觉模式(visual mode)发射。
BMS中上面的(1)是默认模式而(4)即指的疯狗(Maddog)模式
而(2)和(3)暂时?没有在BMS中模拟
在BMS中,(1)模式下是拥有有限的HOJ能力,尽管尚不清楚该捕获模型是否接近真实中的120。
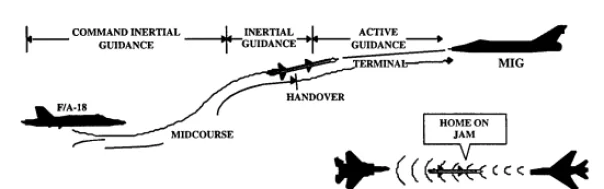
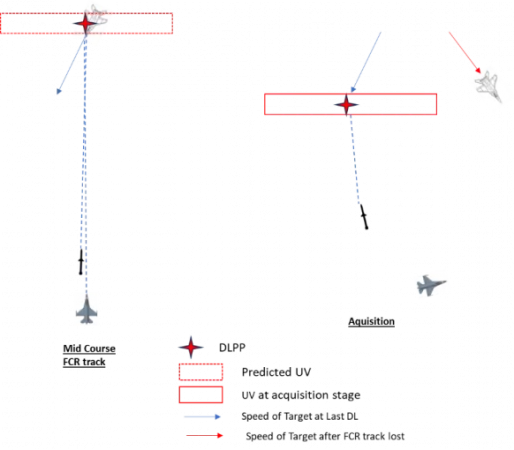
AIM-120在整个飞行过程中有三段的目标引导阶段(见图一)
中段(MIDCOURSE)使用无线电数据链从发射机获取目标信息
目标交付(HANDOVER)阶段,也叫做搜索阶段,会从HPRF搜索阶段开始直到MPRF搜索阶段(详见第八章)。在此阶段下导弹将使用它自身的弹载雷达来对自身引导。" 它能够对多个目标进行分类,并为每枚发射的导弹挑选单独的目标,以打击未解决的目标群"[1]
末端阶段(TERMINAL):末端阶段将使用弹载雷达来引导自身。
不确定区域
从[1]可知
“AMRAAM的设计意味着它非常的依赖来自宿主机传来的目标信息的质量。导弹应具有高度的目标选择性,换句话说:想要只打击所要打击的目标,而不是锁定就近的目标的话,导弹必须严格听从宿主机的指令。导弹的目标信息是由宿主机从单路射频数据链发来。由于导弹非常严格地遵循主机的雷达指令,因此错误的指令将显着降低导弹的有效性。电磁干扰将会显著的压制飞机的雷达跟踪目标能力,这也是导致导弹数据链所接收到的数据质量下降的原因。这样 AMRAAM 会搜索数据链路提供的点的周围的一个区域,称为不确定区域(Uncertainty Volume)。
“不确定区域”是一个指在导弹进入HPRF和MPRF阶段会去搜索的区域。此概念是建模方向的一个重点。
这就是我们必须在系统链中引入误差概念的地方。
雷达精度
- 参考文献[2]中:"精确度是指某一平台在某一特定时间的估计或测量所得到位置和/或速度与其真实位置或速度之间的一致程度"。
- 参考文献 [3]中: "雷达数据链的主要功能是向导弹提供目标的角度、位置和速度信息。位置和速度的测量和传输误差体现了雷达性能的随机性"。
雷达本质上很容易在方位/高度/距离和速度信息的测量中出现误差(基于角偏差率和距离偏差率)
数据链
参考文献[3]“在测量与传输阶段的误差表现了雷达性能的随机性”
惯导(INS):飞机与导弹都自带有惯导系统,这些系统本身自带误差和偏差。且导弹还存在自有误差,这是因为目标信息是来自宿主机,但飞机与导弹间两套INS系统间也存在固有误差,这个误差将会带入传输来的目标信息中。
AMRAAM弹体[1]
所有这些误差都是在对目标的位置、距离、速度和航向进行评估时产生的,所有这些误差都具有随机性,也就是说它们都是不确定值。也就是说,一枚拥有完全精确的目标信息的导弹在使用同一套雷达,同个目标和同个外部状况下发射时也会产生大小不定的误差。
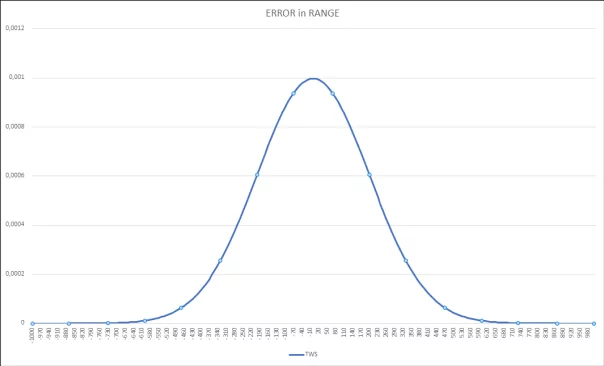
图3展示了距离误差率的性质,我们使用了同样的飞机执行了多轮测试来进行AMRAAM的硬件在环(HWIL)模拟[3]。请注意图三中不同次模拟甚至是通次模拟间测距偏差率的变化。
AMRAAM随机性[1]
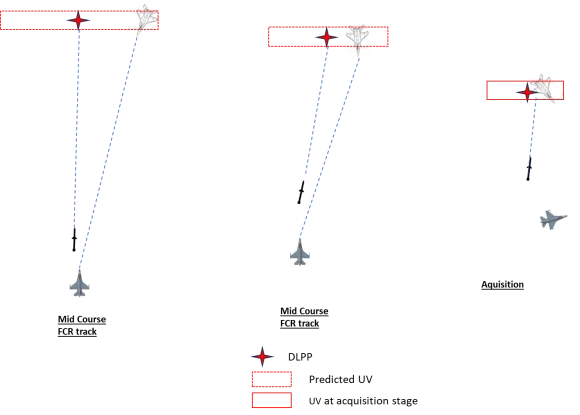
在实战中这些代表了什么?这代表了导弹正在接收目标信息,让我们将这些目标信息称作“数据链提供的点”(DLPP),导弹将会导引到这些点。实际上,由于自有误差的关系,DLPP点位和目标实际上所在位置有可能会不一样。
但是,导弹实际上是“知道”DLPP不是目标,所以它将“搜索”不确定体积区(UV),然后只在该区中进行目标选择:
“AMRAAM 在DLPP周围搜索一个称为不确定体积区(Uncertainty Volume)的区域[1]。”
尽可能准确地估计不确定体积区是一个至关重要的问题,因为正如文献[1]所述:"导弹应具有高度的目标选择性,就是只击中所需的目标,而不是就近目标...... "导弹需要具有目标选择性。
正态分布模型
在开始论述BMS的建模前,我们首先谈谈统计学。
我们可以看到,整个过程中产生的误差具有随机性。
解决这种情况最常见的方法是使用正态分布,也称为高斯分布。
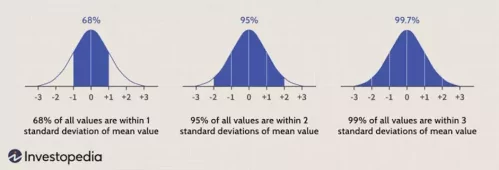
正态分布的特征是“μ”代表分布的平均期望,σ 代表“标准差”。
例如,如果测距偏差的分布为 (µ = 0 , σ = 200ft)。 这代表:目标在DLPP点约200ft范围内是68%的概率,目标在DLPP点的400ft范围内是95%的概率,而目标位于DLPP点600ft范围内则是99.7%的概率
BMS误差模型
标准差
迄今为止,整个引导过程中(雷达/数据链/INS/其他?)的标准差尚不明确。 我们可以做出一些假设,这些假设只是我们的猜测,但根据现有数据可能不会相差太远:
很不幸的一点是,参考文献[2]的数据已经经过了归一化处理,我们无从得知原始数据。不过,这些归一化后的数据仍能在之后的过程中发挥作用。
参考文献[3]中给予了一部分某型号雷达的信息,之中的一部分是军用的搜索与跟踪雷达,它们中的一部分拥有TWS(边跟踪边搜索)能力,如BOR A 550,有些是AESA(有源相控阵雷达)如GM 400。
| 雷达型号 | 方位精度 | 距离精度 | 高度精度 |
|---|---|---|---|
| BOR A-550 | <±0.3° | < 20 m | |
| LANZA | <±0.14° | < 50 m | 340m ≈ 1150ft (100Nm时) |
| GM 400 | <±0.3° | < 50 m | 600m ≈ 2000ft (100Nm时) |
| RRP-117 | <±0.18° | < 46.3 m | 100m ≈ 3000ft (100Nm时) |
| MSSR-2000 | <±0.049° | < 44.4 m | |
| STAR-2000 | <±0.16° | < 60 m | |
| 其他 | <±0.25° | < 25 m |
尚未找到有关速率和目标速度误差的数据,因此我们必须进行估计,并希望我们不会偏离太远。
在此阶段,尽管存在一些高度误差,但目前尚未实现,BMS 模拟的是面上的误差而不是体积上的误差。 这意味着目标的高度目前始终是准确的。 如果当前模型被证明是稳定的话,以后的版本中我们可能会实装此功能。
必须注意的是,每个 FCR 子模式都有不同的自有误差模型。附录 1 对此进行了更详细的讨论。
还需要注意的是,BMS 并不单独对每个误差(雷达/DL/INS)进行建模,而是将整个系统的误差视为一个整体,因此数据可能不会仅与雷达误差直接进行比较。 换句话说,整个系统的标准偏差高于单独雷达的标准偏差。
在此阶段,所有雷达/系统都具有相同的标准误差参数。 可以为雷达数据文件中的每个雷达进行配置。 (注意:如果自行改变这些参数将迫使BMS开发组花更多时间在反作弊开发上,这将拖累修复BUG和实现新功能的进度,所以请遵守多人规则)。
| BMS APG-68(V4) AIM-120 数据链 | 方向精确度1σ | 距离精确度1σ | 速度矢量精确度1σ |
|---|---|---|---|
| STT模式下 | 0,2 deg | 26m | 15 ft/sec |
| SAM模式下 | 0,3 deg | 43m | 20 ft/sec |
| TWS模式下 | 0,65 deg | 61m | 50 ft/sec |
模型的实现与不确定性体积区
误差是在何时引入?如何引入? 前所述,如 [2] 所述,每个数据链提供的目标位置的误差都不同(以图 3 为例)。这意味着,在现实中,数据链提供的目标点可能在某一时刻非常接近目标,但过一段时间后,又开始出现明显偏差。
目前,BMS 会在发射导弹时确定其固有误差,并在发送的每条数据链中应用随机噪声的乘法因子(μ = 1.0,σ = 0.015)。
所有受随机偏差影响的数据(方位角、仰角、射程、速率/速度)都有一个基于高斯模型和标准偏差的独立随机选择(如上面的表2),这些数据在整个导弹飞行过程中将保持不变(噪声作模数)。
如图7中,每次在TWS下发射的导弹,都有:
- 68%几率数据链提供的目标位置与实际目标位置差小于61米(200ft)
- 95%几率数据链提供的目标位置与实际目标位置差小于122米(400ft)
- 99.7%几率数据链提供的目标位置与实际目标位置差小于183米(600ft)
同样的方法也适用于角度误差(方位角)和速率/速度。
数据链提供的位置(DLPP)是实时计算,将会引入目标的实际位置和速度,并将发射时确定的角度、速度、距离误差加入其中。
请注意,这些角度偏差始终是从发射导弹的飞机的角度来看的(因为火控雷达在发射机上),因此发射机离目标越近,横向位置误差自然就越小。
[math]\displaystyle{
横向误差(ft)=距离(ft)*sin(方位角误差)
}[/math]
如例子中,假设方位角误差为 0.3 度,则 40 海里处的横向位置误差为 1272 英尺,15 海里处的误差仅为 477 英尺。
信噪比的影响
根据文献[4]所述,信噪比对测距精度的影响系数为
[math]\displaystyle{
\delta R=\frac{C_0}{2B\sqrt{2 SNR}}
}[/math]
不过,由于 BMS 代码中的信噪比与源信噪比的单位存在不确定性,目前信噪比的影响只是信噪比为1时乘数为0.9(在 BMS 代码中,如果信噪比低于 1,目标将无法检测到目标)到信噪比为4时乘数为1.1。这将在之后的版本中完善。
不确定性体积区
我们在此模型中,假设有一枚AIM-120正在飞行路程的中段,正在飞向由机载雷达持续更新的(每0.5s - 1.0s[1])数据链指定点。
在路程中段的某时刻,导弹将激活弹载雷达的HPRF(高频脉冲搜索)并在之后切换为(中频脉冲搜索)。(参见第八章获取更多内容)。这些搜索模式将会进入具有不确定性的区域(UV),该搜索将在不确定区域(UV)内进行,该区域内的任何目标都将被视为潜在锁定目标。
图6画出了不确定性体积区内角度误差分布与STT和TWS模式下偏差模型的对比(同样使用与距离误差的分布模型)。
在没有任何可用信息的情况下,BMS 不确定性体积区覆盖范围基于 TWS 偏差模型的 2.5 x σ(见图 8),换句话说,不确定性体积区将覆盖所有随机误差的标准偏差的 2.5 倍。
| UV大小 | 宽 | 长 |
|---|---|---|
| – | 距离 * sin (2 * 0,65) | 2 * 61 m = 122m |
| – | – | – |
| 导弹发射机距离-HPRF/MPRF的目标 | – | – |
| 15 | 648 m | 122m |
| 20 | 833 m | 122m |
| 25 | 1037 m | 122m |
| 30 | 1259 m | 122m |
请注意,由于 UV 宽度是根据距离和方位角计算的,因此 FCR 越接近,UV 宽度就越小(参见图 9)。因此,弹载雷达搜索时UV区的大小取决于最后收到的包含导弹发射机和目标之间距离信息的数据链信息。
此时最大的问号是:UV区的分布范围是否也应该取决于 FCR 子模式(即每个子模式的 2.5 x σ)?这是有其道理的,因为这样只会增加目标的选择性,而不会影响到导弹的引导概率。然而,在该阶段,UV区分布范围(以及尺寸)与 FCR 子模式无关,即所有 FCR 子模式中的目标选择性是相同的。
在未来的BMS版本中可能会提高STT和TWS子模式下的目标选择性。
引导概率
连续中段引导
在此场景中,导弹将一直保留接收到的目标信息直到导弹到达HPRF/MPRF阶段,BMS模型将根据构造输出:
STT引导为100%的概率 TWS模式为98.7%的概率 机载雷达不同的子模式间的选择性相同 导弹发射机与目标越近,导弹的选择性越好
不过等等,我们是不是忘了速率偏差和速度偏差?
实际上我们没有忘记,因为每条数据链信息都包括DLPP位置,因此在战机锁定敌机时,此误差不会在引导概率中发挥作用。然而,这些目标速度误差会在制导系统中生效。 也就是说,导弹在中途可能会以非理想的轨迹飞向DLPP位置。就引导概率而言,只有你在导弹开启弹载雷达前就脱锁时,速度和速率误差才是该考虑的问题,这是下一章讨论的主题。
导弹中段FCR丢失锁定时的情况
在导弹位于中段时载机的FCR丢失对目标的锁定时,导弹将再也不能获取并更新DLPP。此时导弹将进入惯性导航状态,导弹将会从来自最后一个数据链信息包的DLPP位置进行插值计算。
当导弹到达相对插值后DLPP位置的HPRF/MPRF距离后,导弹将依据插值DLPP正常进入HPRF/MPRF搜索并搜索不确定体积区。
非机动目标
机动目标
小结
估算导弹在中段引导时丢失数据链后的引导几率(PG)是非常复杂的,这是因为想要估算脱锁后的引导几率需要同时考虑到:随机误差、脱锁时与敌机的距离、速度和方向。
其实计算出引导几率数据还是有可能的,只是想要计算的话你必须使用计算程序在不同的配置下计算上百轮发射的模拟。但是这已经超出了BMS的范围。
不过,在导弹中段引导丢失时,以下的结论还是成立的
- 数据链传输维持的越久,引导几率越高
- 目标机动越剧烈,引导几率越低
- STT模式的引导几率 > SAM模式的引导几率 > TWS模式的引导几率
- 数据链传输维持的越久,导弹的选择性越大
在中段引导和干扰源追踪(HOJ)下脱锁
在中段引导时,如果目标开启了电磁干扰(Jamming), 导弹会将其作为潜在的HOJ目标。
为了防止宿主机脱锁,导弹将会将目标的干扰信号作为引导信号来更新DLPP位置。
HOJ引导同样包含有自有误差:
| AIM-120 HOJ | 相对方向的精度 1σ |
距离的精度 1σ |
速度矢量精度 1σ |
| HOJ | 0.8° | 122m | 100 ft/sec |
在导弹处于HOJ模式时的引导几率小于火控雷达锁定目标时的几率,但是在脱锁时,导弹仍然可以在HOJ模式下维持很高的引导几率,特别是目标在机动时
目标交接(Handover)/索敌(Acquisition)方法
AMRAAM的表现对其制导解决方案中最后一个接收到的数据链最为敏感。导弹使用的最后一个数据是最后接收到的数据流中的数据之一,但不一定是最后一个数据。在基于多个参数的特定距离内,AMRAAM 将会停止将接收到的数据纳入其制导解决方案中[2]
我们现在假定导弹在进入MPRF(中脉冲重复频率)后就不再接收数据链信息。
HPRF(高脉冲重复频率)
如果导弹相对DLPP位置的距离已经到达了切换到HPRF搜索的距离,AIM-120将对处于其引导头视场内的所有目标执行一轮搜索序列
HPRF目标选择标准:
- 目标被忽略的情况:
- 目标位于不确定体积区外
- 目标信噪比小于1
- 目标近距离为正
- 目标方位角为正
- 剩下不满足以上任一情况的目标都为被选择目标
在HPRF模式下,导弹数据链仍然可以接受来自宿主机火控雷达的目标位置信息
在 HPRF 搜索/引导阶段,可能会出现以下几种情况:
- 如果HPRF阶段搜索后未找到目标,导弹将继续飞向 DLPP(如果目标仍被索敌,则位置根据 FCR 更新;如果目标已脱锁,则根据最后已知数据链信息进行插值)。
- 如果HPRF阶段导弹找到了目标,导弹便直接向目标位置引导
- 如果虽然HPRF阶段找到了目标,但是在引导过程中丢失目标(如目标正在逃离(对应简语:Cold))那么:
- 如果目标仍然被宿主机锁定,那么导弹将会继续导航到新更新的DLPP位置
- 如果目标脱锁,那么导弹将会引导到根据最后已知的HPRF搜索到的位置进行插值的所得结果上
MPRF(中脉冲重复频率)
在距离目标多远时进入MPRF阶段是靠F-16的SMS页中目标大小的设置而确定的。
在导弹相对DLPP的距离满足进入MPRF阶段时,导弹将会对导引头视场内所有目标进行一轮搜索序列
在MPRF阶段,即使宿主机仍然维持锁定目标,此时的导弹也会停止接收数据链。
MPRF阶段的目标搜索标准:
如果存在HPRF目标,则导引头将会切换到MPRF模式,将HPRF搜索到的目标作为MPRF目标。此时导弹将不再进行搜索序列。
如果无HPRF目标,则导引头会对视场内的目标进行搜索序列。
目标被忽略的情况:
- 目标不在不确定体积区
- 目标信噪比小于1
- 在剩余的合法目标中已选择了离DLPP位置最近的目标。
如果未找到 MPRF 目标,只要导弹与DLPP(插值)的距离大于 0.5海里时,导弹会继续以同样的目标搜索标准执行搜索序列。在与DLPP的距离小于0.5海里时,若仍未找到 MPRF 目标,则导弹便彻底无效(lost)。
小结
将Falcon 4.0中超·简单的AIM120系统模型改成现在的对真实120系统的简单模拟已经是非常的辛苦,这项工程已经花了我们不少时间,不少头发和好几升的咖啡。
理解和猜测真实武器系统如何工作不仅具有挑战性,而且从代码执行的角度来看也很难建模。
第一版的AIM120索敌建模只是获得了部分的成功(4.37.0版本),我们尝试了使用PG(引导率)来模仿aim120的特性,其中我们低估了过程中的随机性对结果的影响,而不是直接对其运作原理进行建模,我们尝试了引用适当的高斯分布来将其模拟效果做到最好。
我们对 "不确定体积区 "概念的理解也有偏差,并对 HPRF/ MPRF 搜索标准做出了错误的假设。
但另一方面,此建模的随机性使得测试也变得相当困难,我们必须要执行上百次对场景的模拟才能得到统计学上的结果。
我们非常感谢BMS社区中的志愿者对早期版本的新模型的测试,每次你们使用Tacview报告并复现导弹奇怪的表现时,我们才能意识到错误并修复建模。
现在AIM-120的建模仍然有很多需要提升的地方,比如,两种AIM-120发射模式的表现暂未实现,但我们相信 4.37.3 中包含的新版建模(如本文档中所述)将为你带来更有趣游戏体验。
附录1
机载雷达(FCR)子模式误差建模
在与现实中的飞行员讨论时,他们总是一致认为,尽管TWS提供了同时跟踪并引导多个目标的功能,但他们总是将STT作为“首选的”制导FCR子模式。
经过研究,与此相关的最重要文章是:(“Optimization of Electronic Protection Testing for the F/A 18 active Guidance Air to Air Weapon system”A Thesis Presented for the Master of Science Degree The University of Tennessee, Knoxville,Cassidt Clayton Norman Dec 2003)(“优化F/A 18主动制导空对空武器系统的电子保护测试”)
该文件与 BMS 相关,因为它涉及AIM120与APG68的同代雷达(即 APG65 和 APG73)的协同。
此论文主要研究电子攻击(EA)对雷达/AIM120系统的影响
文中内容:
“1996年,美国海军资助了武器系统的评估计划,其中包括对F/A-18和AMRAAM武器系统进行电子保护(EP)测试。 目前的测试方法包括使用对空训练版AMRAAM来攻击采用特定的电子攻击技术的全尺寸目标。在飞行过程中记录导弹和雷达的数据链,并在 硬件在环(Hard-Ware In The Loop,HWIL)仿真中进行复盘,以测试导弹在模拟拦截相同电子攻击威胁时的性能。每次试飞都在 HWIL 中执行 20 次模拟,以计算导弹制导概率(Po)。 每次HWIL模拟都要执行50次实弹模拟,以计算武器有效性概率(PWE)。表格和图表均不包括与计算概率相关的不确定性。” (<= too bad for us…)
由于该论文属于公有领域,它隐藏了许多信息,此文章甚至没有透露被测试的不同电子战手段的技术区别。
论文还指出,至少在当时,PG的不确定性非常高,他们试图通过使用几种技术和NAVAIR武器部门的中国湖F/A-18雷达实验室来改进他们的认知。
文中还提到:
“A closer look at the test methods revealed that only a few tests of aircraft radar are used to characterize aircraft radar performance versus the EA threat while thousands of simulations are used to characterize AMRAAM performance. For the average number of test runs of each radar mode, the uncertainty associated with the aircraft radar performance calculation was found to be± 43.6% while the uncertainty associated with AMRAAM performance calculation was found to be± 1.39% (using 95% confidence interval). The combined uncertainty is± 44.4%, which spans a wide range of performance for any calculation of PG or PWE.”
我们第一次看到,他们每种雷达模式都经过了单独测试。这代表,FCR子模式间的PG值可能大相径庭。如果测试结果明显相同,为什么还要对每种FCR子模式都要进行数百次不同的测试呢?
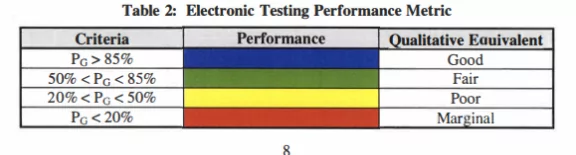
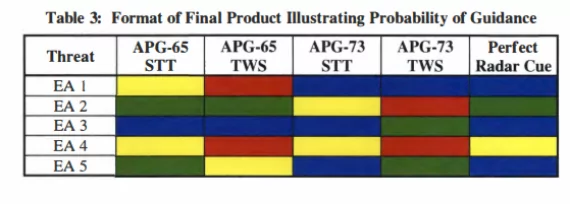
论文中的表3更为明显,它用颜色代码标出了每种雷达和FCR子模式的PG值。
我们必须意识到,此论文只是个示例,它可能会,也可能不会透露任何相关信息。此外,它提供的是与“电子战”相对应的结果,而在 BMS 中,我们更感兴趣的是没有不受电子攻击手段影响的结果。
TWS的PG值几乎总是低于STT,这可能也是种巧合......但也可能不是。
不过,在这一阶段,很明显,HWIL(Hard Ware In the Loop)或NAVAIR武器部门的中国湖F/A-18雷达实验室并不认为STT和TWS具有相同的性能,否则又何必多此一举呢?这里面显然有问题!
误差和变化率误差分析
请参阅论文2中的附录A
为了确定子模式下雷达的工作方式是遍历还是静态的, 他们对距离误差和距离变化率误差进行了一定量的测试。
遗憾的是,为了掩盖武器系统的真实误差,误差被归一化了。然而,对我们来说有趣的是,误差图可以进行比较,因为它们使用了相同的归一化处理。
我们还必须认识到,所有的这些测试都是在战斗机在使用电子战技术的情况下完成的,遗憾的是没有绘制非电子战目标的测试作为参考,除非这些测试中存在一次测试就是非电子战条件下的测试?这我们永远都不会知道。
总之,我们对此论文的每张图表都进行了对比,并试图评估STT和TWS之间的差异是否一致。
如果在如此多的运行和飞行案例中都发现了明显且一致的差异,我们或许可以得出结论:STT和TWS具有不同的工作流程,这使得它们PG值完全不同。
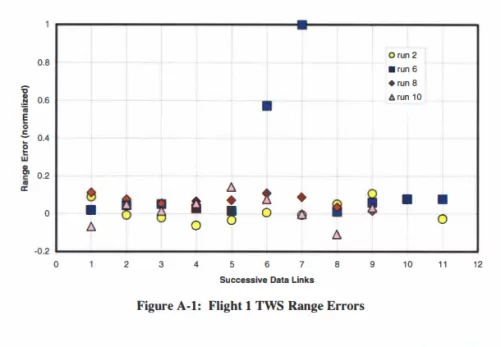
误差范围
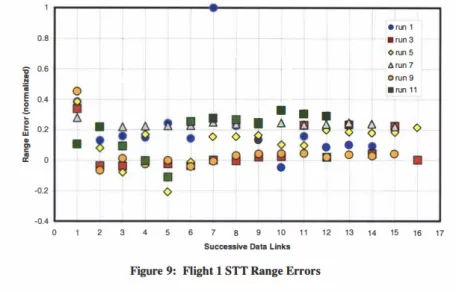
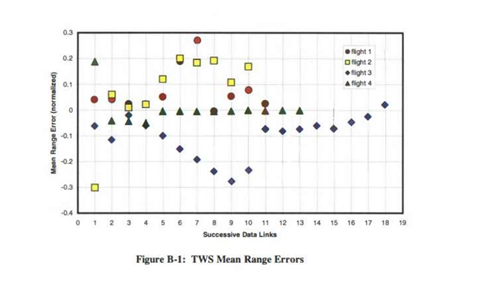
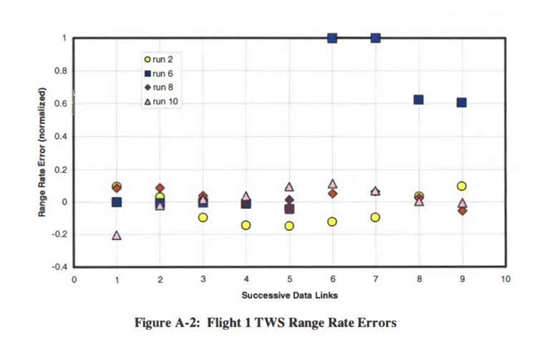
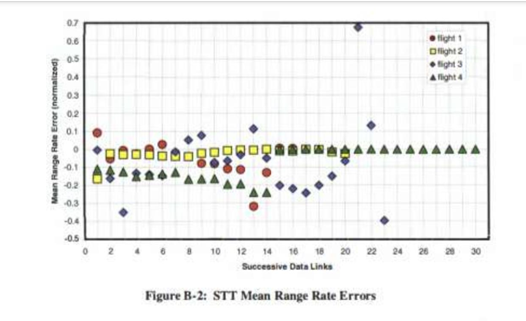
Flight 1的STT和TWS没有明显差异,但TWS有两个奇点。
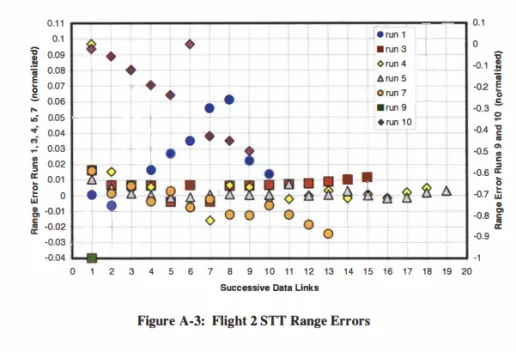
Flight 2的STT与TWS模式测距误差存在显著差异
- 第1、3、4、5、7次测试(STT):误差范围介于-0.03与+0.04之间
- 第9-10次测试(STT):误差范围介于-0.04与+0.1之间
- 第2、6、8、12次测试(TWS):误差范围介于-0.25与+0.45之间
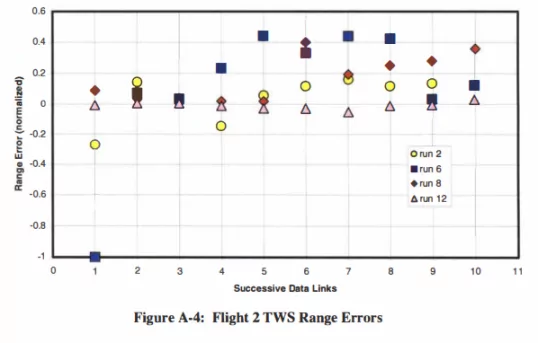
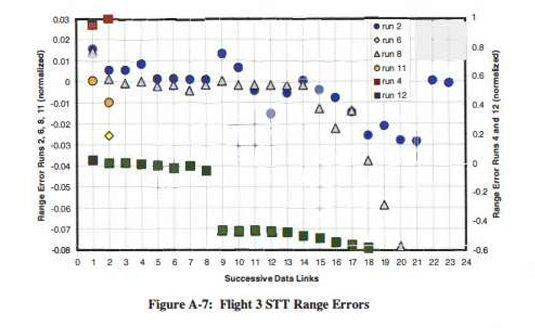
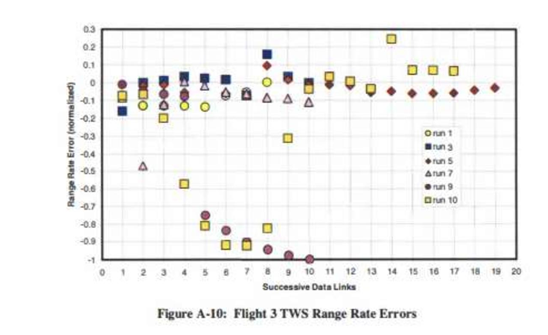
Flight 3的STT与TWS模式测距误差存在显著差异
- 第2、6、8、11次测试(STT):误差范围介于-0.08与+0.015之间
- 第4-12次测试(STT):误差范围介于-0.08与+0.03之间(或更高)
- 第2、6、8、12次测试(TWS):误差范围介于-1.0与+0.2之间
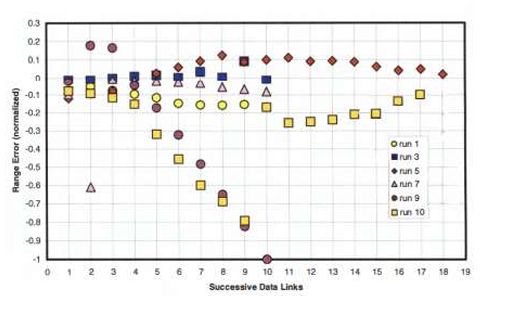
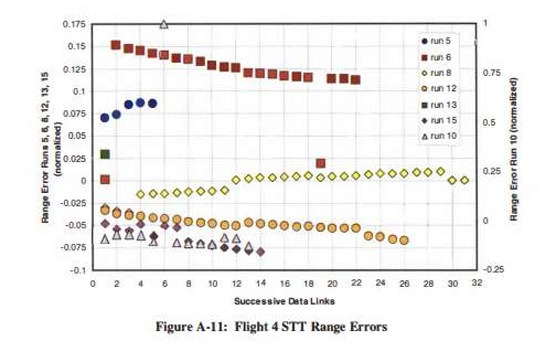
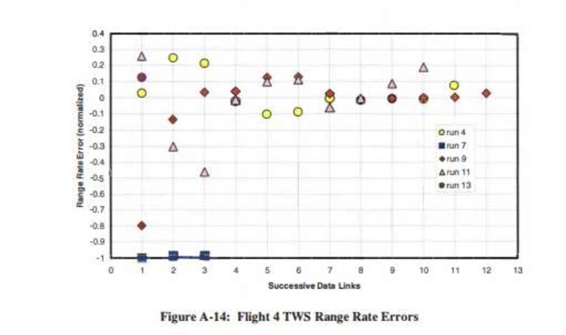
Flight 4的STT与TWS模式测距误差存在差异
- 第5、6、8、12、13、15次测试(STT):误差范围介于-0.05与+0.15之间
- 第10次测试(STT):误差范围介于-0.10与0之间
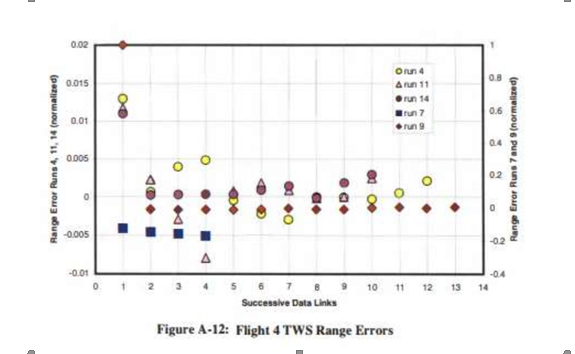
- 第4、11、14次测试(TWS):误差范围介于-0.0005与+0.0125之间
- 第7-9次测试(TWS):误差范围介于-0.20与0之间
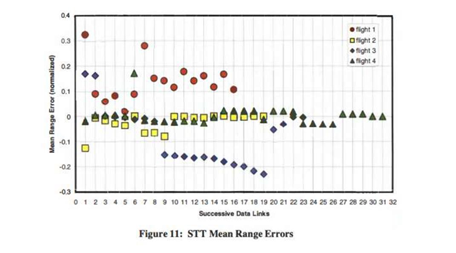
平均测距误差
- 综合所有误差范围可知,TWS模式的平均测距误差分布区间宽于STT模式
- 31条数据链报文中,STT模式有5个数据点超出-0.2 / +0.2区间
- 19条数据链报文中,TWS模式有10个数据点超出-0.2 / +0.2区间
- 结论:在测距精度方面,STT模式性能优于TWS模式
测距误差率表现
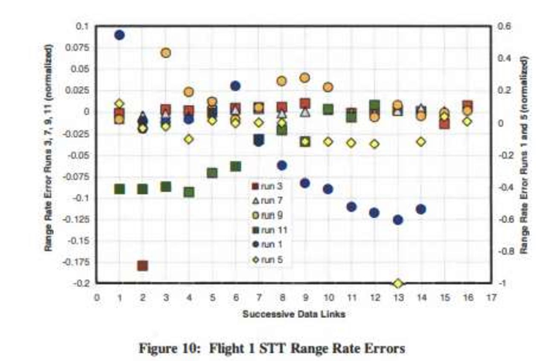
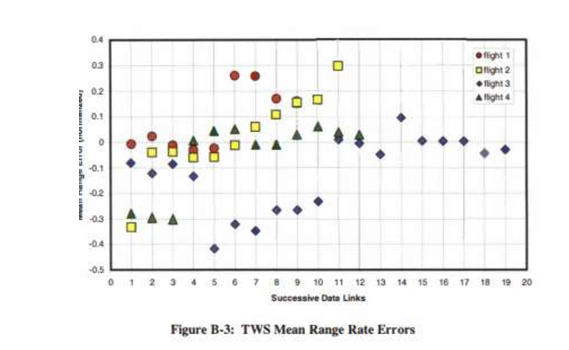
Flight 1的STT与TWS模式测距误差率存在显著差异
- 第3、7、9、11次测试(STT):误差范围介于-0.1与+0.05之间
- 第1-5次测试(STT):误差范围介于-0.60与0.2之间
- 第2、8、10次测试(TWS):误差范围介于-0.2与+0.15之间
- 第6次测试(TWS):误差范围介于0与+1.0之间
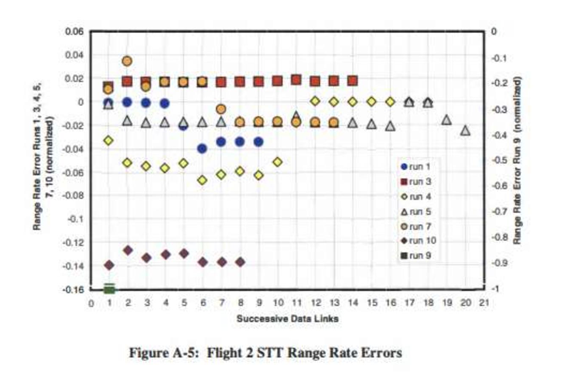
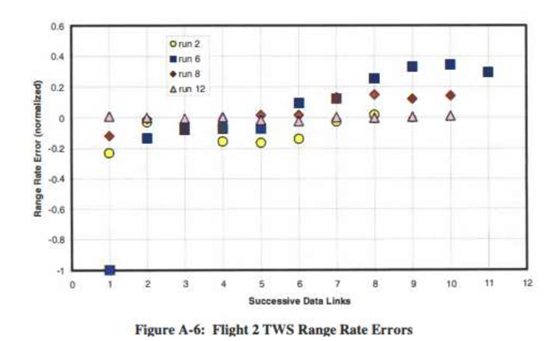
Flight 2的STT与TWS模式测距误差率存在显著差异
- 第1、3、4、5、7、10次测试(STT):误差范围介于-0.16与+0.02之间
- 第9次测试(STT):数据难以分析
- 第2、6、8、12次测试(TWS):误差范围介于-0.2与+0.35之间
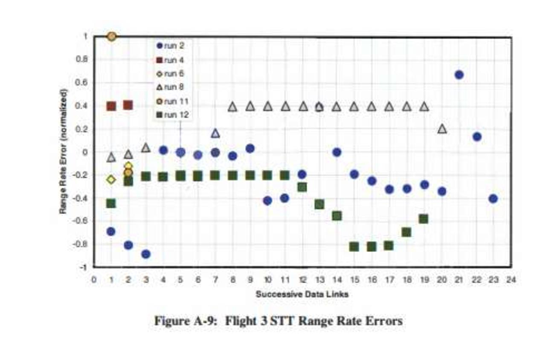
Flight 3的STT与TWS模式测距误差率无显著差异
- 第2、4、6、8、11、12次测试(STT):误差范围介于-1.0与+0.4之间
- 第1、3、5、7、9、10次测试(TWS):误差范围介于-1.0与+0.3之间
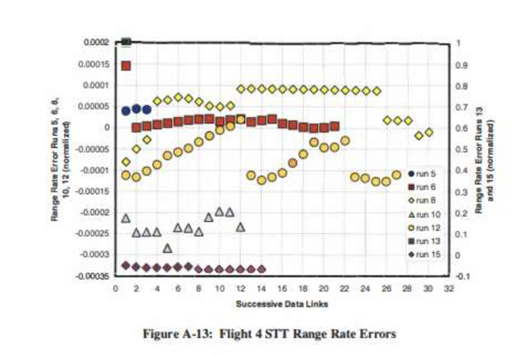
Flight 4的STT与TWS模式测距误差率存在显著差异
- 第5、6、8、10、12次测试(STT):误差范围介于-0.0003与+0.0002之间
- 第13次测试(STT):误差范围介于-0.1与+0.0之间
- 第4、7、9、11、13次测试(TWS):误差范围介于-1.0与+0.25之间
平均测距误差率
- 综合所有测距误差率范围可知,TWS模式的平均测距误差率更大且分布区间更宽(STT区间:-0.4 / +0.1;TWS区间:-0.4 / +0.3)
- 结论:在测距率精度方面,STT模式性能优于TWS模式
参考资料
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 “Distribution Simulation Testing for Weapons. System Performance of the F/A 18 and AIM120 Amraam” LCDR Tom Watson , Naval Weapons Test Squadron, Point Mugu CA https://apps.dtic.mil/sti/pdfs/ADA355385.pdf
- ↑ 2.0 2.1 2.2 Radartutorial.eu https://www.radartutorial.eu/01.basics/Radars%20Accuracy.en.html
- ↑ 3.0 3.1 3.2 “Optimization of Electronic Protection Testing for the F/A 18 active Guidance Air to Air Weapon system” A Thesis Presented for the Master of Science Degree The University of Tennessee, Knoxville Cassidt Clayton Norman Dec 2003 https://trace.tennessee.edu/cgi/viewcontent.cgi?article=6680&context=utk_gradthes
- ↑ Wikipedia: normal distributions https://en.wikipedia.org/wiki/Normal_distribution
| ||||||||||||







 沪公网安备 31011002002714 号
沪公网安备 31011002002714 号