电路教程(进阶篇)

首页 > 教程 > 电路教程(进阶篇)

短 刷 阅 编 历

本文来自：贴吧
原作者：(御道风云)
原视频/文章地址：http://tieba.baidu.com/p/5293320777

MediaWiki:Timer

12020/04/02 13:33:0本文上次更新 ，请注意文章时效！

摘要：

• 内容概述：
  • 通配符基础以及一些电路的技巧和设计方法.
• 说明：
  • 在你阅读本篇时,默认你已经对前面的入门篇和基础篇了解并掌握.
  • 基础篇链接:电路实例教学(基础篇)

• 那些基础篇先收藏慢慢学的同学,看~我又写了一篇 (:逃.
• 拖了好长时间,实在怕在过一段好多东西都忘了,
• 趁还有点东西,还是尽快把自己掏空吧,.
• 祝大家电路(zhuang)玩(bi)的开心.

第一部分 通配符基础

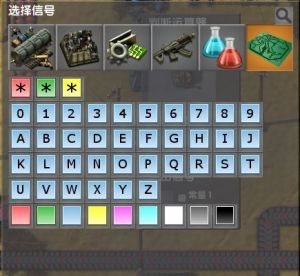
• 打开信号栏,上图第一排的3个*形状的信号就是通配符
• 鼠标放上去,可以看到说明:
• 红色*信号=所有信号
• 绿色*信号=任一信号
• 黄色*信号=每个信号

• 丨通配符的作用是用于对多个信号进行同一处理丨
• 来看一下具体怎么用.

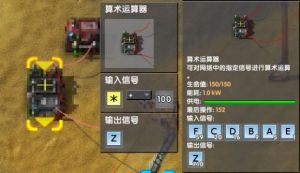
算数运算器

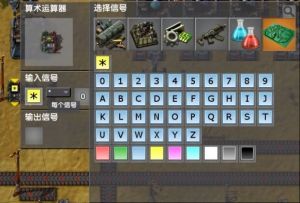
• 点开算数运算器,可以在输入信号的右栏设置为黄色*信号,
• (只能在右栏设置,算数运算器只能使用黄色*信号)
• 同样的,也可以在输出信号栏设置为黄色*信号
• (输出栏设置为*信号必须以输入栏使用黄色*信号为前提)

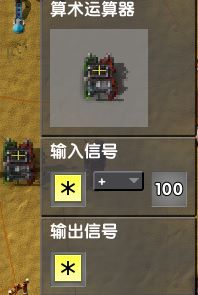
• 这里以(输入 *+100;输出 *)为例
• (因为只能用黄色*信号,就不额外说明*的颜色了)

• 在一个常量箱里随便设置一些信号连上算数运算器.
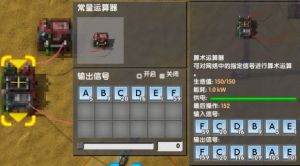
• 通过算数运算器显示的输入输出,可以看出这里运算器的作用是:
• 对每个输入的信号都进行+100,再将每个信号输出.
• 黄色*信号=每个信号

• 接下来将输出信号改为Z信号,
• 可以看出这里运算器的作用就是
• 对每个输入的信号都进行+100,再将每个信号以Z信号输出.
• 将(F,59)+100输出为(Z,159),将(C,20)+100输出为(Z,120),依此类推
• 所有Z信号相加就是(Z,710)了.
• 一句话总结,
• 黄色*信号:对每个信号单独进行同一处理(用于算数运算器)

---

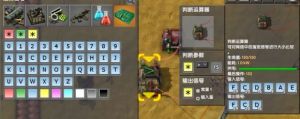
判断运算器

• 点开判断运算器,类同算数运算器,可以在输入信号的右栏设置为红色/绿色/黄色*信号

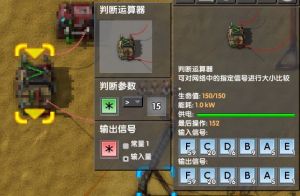
• 先以判断 黄色*＞15;输出 *-输入量)为例
• (同样的输出栏设置为*信号必须以输入栏使用*信号为前提,后不赘述)
• 由图可以看出黄色*的作用跟上文类同
• 黄色*信号:对每个输入的信号都执行一次---如果符合条件,则按设置的输出信息进行信号输出(用于判断运算器)

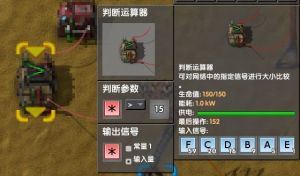
• 这里使用了绿色*信号(任一)和红色*信号(所有)
• 此时判断运算器的逻辑是:
• 在输入的信号中,只要有任何一个信号符合＞15,那么就将所有的信号(值为输入量)输出.
• 一句话总结
• 绿色*信号:在输入的信号中,只要有任何一个信号符合条件,则按设置的输出信息进行信号输出(用于判断运算器输入栏)

• 最后一个红色*信号,举一反三也不难理解
• 红色*信号:如果所有输入的信号都符合条件,则按设置的输出信息进行信号输出(用于判断运算器)

第二部分 3种计算2^n的方法

• 0.15版本给算数运算器加上的幂运算,进一步的降低的电路的使用难度.
• 在"显卡"中,是需要计算2的n次方,之前我做了一些摸索,虽然现在没卵用了,但思路还是有借鉴意义的.

循环电路

• 比如计算2^9
• 如果让我们自己去计算,我们一般会一遍遍的*2,就跟编程中的循环类似.
• 电路也可以按这思路走
• 大致过程如下
• 1 信号M的值为9
• 2 信号N的值为1
• 3 M的值是否大于0? 是-执行第4行 ; 否-执行第7行
• 4 N的值*2
• 5 M的值-1
• 6 执行第3行
• 7 将N的值输出
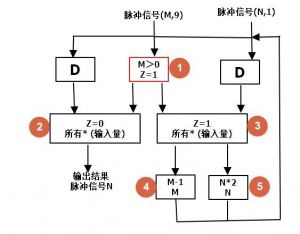
• 根据思路,我们先画出参考电路图

• 做些说明,
• D为delay,延时器.信号怎么输入就怎么输出,即不对信号进行处理.一般为(每个*+0,输出*).
• 使电路信号能够同步.
• 在电路图可以清楚的看出,
• 1号运算器作用是判断;2号和3号进行选择分支;4号和5号进行处理
• 是一个非常简单的循环电路.
• 接着就可以实际测试了.
• 然后轻而易举的就发现了bug,4号运算器有问题.
• 在整个电路还没启动情况下,4号运算器持续输出(M.-1)
• 显然与剧本不符,原因是4号运算器没有接收M信号,则处理时是默认M值为0,即接收了(M,0)
• (M,0)-1=(M,-1).
• 这有点麻烦,不过解决方法也不少.
• 比如,在4号运算器的下面加一个(M≥0;输出M-输入量),把(M,-1)信号给拦下
• 同时在5号下面加一个D,保持信号的同步.
• 不过这样做的话,整个电路流程的运算耗时就会增加1t,本来就3t的耗时,增加1t可不少
• 电路bug修复尽量避免增加耗时.
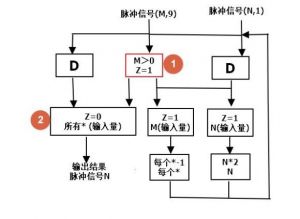
• 其实发现这个问题时,我第一个想到的解决方法是把4号运算器改为(每个*-1,每个*),
• 因为这算是比较经常出现的问题了,我也经验丰富了些.也可以说是通配符运用上的一个小细节吧
• 改之后需要使4号运算器只会接收M信号,所以3号运算器处也要改.
• 上结果:

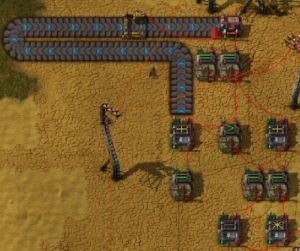
• 最后来一张实际图,

• 没整理,电路有点乱.上面的传送带、常量箱的是为了发出初始脉冲信号.
• 电路成功的输出了信号(N,512),基本成功.
• 循环电路有一个优点,没有存储器,毕竟储存的本质就是信号循环.
• 循环电路将信号保持和信号处理结合了起来,整个电路很精妙,有很强的协调感,很精简,以很少的运算器完成处理.
• 不过缺点也很明显.
• 最后,需要的注意的是,有时候在复杂电路(尤其是循环电路),结果正确不一定过程正确.
• 以上面的为例,有可能除了输出结果(N,512)外还输出其他无关无用的信号,需要拦截或者修改电路.
• 又可能只是在一定范围内能正确的输出结果,一些特殊的情况下就出现问题了.
• 到底行不行,测试起来也是不容易的.

---

取值电路

• 简单思考一下前面循环电路计算2^n的耗时.
• 显然,要计算的值越大,耗时越长.耗时大致等于(3*n)t.
• 这个操作是要用在"显卡"上的,这样一个简单操作,耗时太长,显然无法"商用"的
• 更关键的是耗时不确定,难以做到信号的同步.
• 并没有实用价值.
• 考虑到"显卡"最大只计算2^28,可以换个思路,采用取值电路.
• 丨取值电路,事先将计算结果储存在常量箱,在处理时直接从常量箱里取出结果.丨
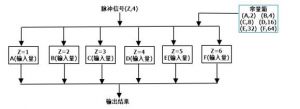
• 这里以计算2^4为例,做一个简单取值电路

• 可以看到,每一个运算器都对应一个值,一种信号,来对应一种计算.
• 因为只有6个运算器,常量箱只有6个结果,因此只能计算2^1到2^6.
• 要计算2^28就需要进行扩展,使用28个运算器,常量箱里写好28个结果.
• 不过这也很容易.
• 这是计算2^28的成品,

• 显而易见,取值电路其实是牺牲"面积"来换取运算速度.
• 1t的运算耗时,真的没有比这快的了.还非常的稳定,不像其他电路动不动出bug.
• 如果你感觉还有太麻烦的缺点,那就错了,你会发现这比去设计电路快多了...
• 自然限制也很多.
• 情况复杂的计算基本是不用想了,
• 计算的情况如果超过游戏所有信号种类的数量,处理起来就会很麻烦.
• 让电路变成体力劳动.
• 还有一些要注意的小问题.
• 最后,
• 取值电路在那些没什么卵用的电路中是很常见的,比如"显卡".
• 关键的还是取值电路的思路
• ———事先计算,用时即取.
• 比如,
• 贪吃蛇电路的信号处理耗时大概有40t,这再优化也少不了太多
• 但电路的操作情况很少,只有保持前进,右拐,左拐3种.
• 可以将电路"复制"3份
• 在等待下一步移动的时候,直接把下一步前进,右拐,左拐3种情况的结果都计算出来,计算具体要显示出来的画面.
• 然后储存下来.
• 到下一步时,根据玩家的操作,从储存3种情况结果直接取出进行显示,取出对应情况的结果进行直接传给"显卡",同时计算下一步的3种情况的结果.
• 理论上至少可以将运算耗时降低到10t以下.
• 设计电路的时候,可以从这些计算是否真的要计算的角度思考一下,有时候真的省好多事.

---

信号匹配

• 循环电路耗时长,取值电路面积大,那么有没有一种...耗时既短又占地小的电路?
• 这时通配符激动的站了起来.
• 通配符的作用是对多个信号进行同一处理,但在大多数情况下,这个"多个信号"都不超过两位数...
• 是时候让通配符展现一波真正的实力了.
• 先说明,其实本质上还是取值电路,只不过是变着法的取结果
• 以计算2^7为例.

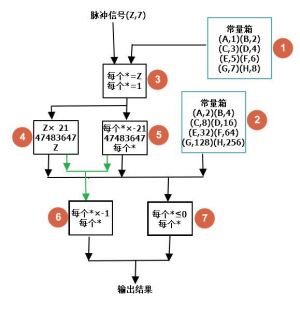
• 先看输入信号,1号常量箱,2号常量箱这三样,
• 能看到明显的对应关系,
• 输入(Z,7),对应1号常量箱的(G,7),(G,7)对应(G,128),
• 如果通过对应关系进行转换,正好得出结果.
• 这就是电路逻辑--使用两级转换来取结果.(你也可以理解为取两次...)
• 7转换为G转换128.完成
• 如果输入(Z,4),
• 就是4转换D再转换16出结果
• 再来看转换是具体是怎么实现的
• --第一步7转换为G--
• 3号运算器使用了所有*,使1号常量箱的每一个信号都与(Z,7)进行比较,最后只有(G,7)符合条件,可以输出.
• 实际上(Z,7)也会被输出,因为"每一个信号都与(Z,7)进行比较"中的"每个信号"也包括(Z,7)信号本身.
• 之所以限制输出的值是1,是因为我们不需要G信号的值,限制为1方便后续电路处理.
• 也就是说,3号运算器输入信号为(Z,7)+1号常量箱所有信号,输出信号为(Z,1),(G,1).
• 同理,如果输入(Z,5)+1号常量箱所有信号,输出信号则为(Z,1),(E,1).

---

• 接着该由信号G转换为128了,
• 信号(G,1)和2号常量箱的(A,2),(B,4),(C,8)等等众多信号输入,怎么样才能最后输出一个(G,128)?
• 这需要三步走———区别、筛选、还原.
• 暂时忽略4号运算器,
• 先看5号运算器,
• 为什么乘以那个莫名其妙的数?
• 为了信号区别.
• 因为游戏里信号值的范围是-2147483648~2147483647.(了解编程的可以知道这是一个int)
• 直观一点就是-2^31~(2^31-1)
• 3号运算器输出的是(G,1),也就是说在5号运算器乘那个数之后,输出(G,-2^31-1).
• 这步的目的是让G变成一个尽可能小的负数,保证在加上一个正数时,不会变成正数.
• 而-2^31-1差不多就是最小的负数了,加什么正数都不可能变成正数.
• 那为什么要干这个?
• 5号运算器的输出与2号常量箱相连,
• 那5号输出的(G,-2^31-1)就会与常量箱的(G,128)相加.结果是(G,-2^31-1+128).
• 在这一群信号输入到7号运算器时,信号G就能"鹤立鸡群"了,
• 完成信号区别,
• 信号G肯定是个负数,而其他信号全是正数.
• 7号运算器一个(每个*≤0)判断,只有信号G符合条件,
• 完成信号筛选.
• 7号运算器输出(G,-2^31-1+128).
• 同时6号运算器将之前的G*-1,输出相反的(G,2^31-1)
• 最后一相加.(G,-2^31-1+128)+(G,2^31-1).=(G,128)
• 结果(G,128).
• 完成信号还原.成功取数.

---

• 还没完,
• 但在实际上,3号运算器输出的是(Z,1),(G,1).
• 5号运算器乘那个数之后,输出其实是(Z,-2^31-1),(G,-2^31-1).
• 这个Z信号最后会跟着结果一起输出...
• 虽然Z信号不影响运算,但我们不需要它.
• 这就是4号运算器的作用,拦截无关信号.
• 原理很简单,5号运算器表不是多输出一个(Z,-2^31-1)吗?
• 那4号运算器就输出一个(Z,2^31-1),一相加不就抵消了吗.
• ---再说明一下信号区别,
• 信号区别,不一定非要用一个最小的负数,
• 例子中因为最大只计算2^8=256,所以随便找个小于-256的就能起到区别的作用.
• 我用最小的负数只是因为方便而已.
• 而且不一定非要正数负数进行区别,
• 这样做的目的只是将信号区别开来,具体可以根据实际情况选用的.
• ----还有很多细节就不费篇幅说明,多思考一下就能发现.
• 这个电路虽然耗时既短又占地小还容易扩展,但毕竟比不上取值电路的1t耗时,
• 工厂又不是北京,地皮不值钱,所以"显卡"使用的还是取值电路.
• 通配符可以开心的去领便当了.

---

• 看完之后,不经有些疑问,
• 我耗费了那么多时间,各位厂长耗费了那么多精力,
• 就是为了学习怎么耗时短又占地小的计算2的n次方?
• 那官方特地扩展电路计算岂不很尴尬?
• 怎么可能.
• 上一篇最后的那个控制火电的小电路是个循环电路,
• 这篇最先讲的就是循环电路的简单设计思路.
• 信号匹配与筛选就是贪吃蛇电路中的"最核心技术"了
• 俄罗斯方块大规模运用取值电路,制作耗时和处理时间至少降低了3成(当然面积也...).
• ......
• 什么,这些电路你都不接触?
• 你是不是走错片场了....

• 还是你只是单纯的想过来-1s?

---

• 接下来总结知识点,

信号匹配

• 信号匹配指通过通配符实现信号值与信号种类的转换.
• 就是上面的1号常量箱和3号运算器起的作用.
• 一个信号值到底应该转换为那个信号种类?
• 这就需要玩家自己在1号常量箱里定义了,
• 比如(G,7)就相当于定义了信号值7可以转换为G
• 具体怎么定义遵循实际情况,尽量做到方便.
• 记得我看到过一个问题,
• 有100种信号,分别储存着不同的值,
• 怎么样让每个信号的值都加上它前面的那个信号值?
• 信号匹配就是解决方法.(别告诉我你不会反向处理...)

通过抵消法来清除无关信号

• 使用通配符与一种信号进行比较经常会将信号自身也输出.
• 这个信号通常是无用的,在一些情况甚至会干扰处理.
• 通过并排加上一个运算器,输出相反的值,
• 在信号网络中正负抵消,使值变成0,将该信号清除.
• 看上例,为什么不在3号运算器左边加一个输出(Z,-1)的运算器进行抵消,
• 而是在5号运算器那一步进行抵消?
• 因为在Z值不确定的情况下,无法用一个运算器输出信号(Z,-1).
• 通配符玩的多了,这个问题很快就能成为"熟人".

信号筛选

• 信号筛选指在众多信号中取出指定信号种类的信号值.
• 这可以算的上是高端操作了,你也可以理解为"大佬级"操作.
• 这个操作还有点上限.
• 来个(hao)小(nan)问题,
• 如果2号常量箱的值有正有负,也没啥规律.(不重复也不为0)
• 那怎么样才能把指定信号种类的值筛选出来?
• 虽然思路很好确定,但可不好做.

第三部分 电路的信号同步

• 电路设计应尽量遵循信号同步原则.(名字什么的仅供参考理解)
• 信号同步即电路中的所有信号在时间上保持同步.
• 不太好理解,这里举个例子
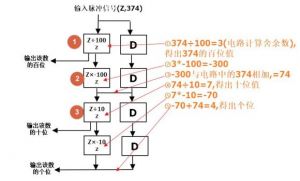
• 这是一个入门级电路,用于将一个三位数分解为百位,十位,个位

• 相信都能理解,
• 可以看到电路的右边整齐的排着4个D,之前说过D时延时器,不对信号进行处理.
• 但为什么要有延时器这东西?
• 因为(Z,374)这个信号除了进行1号处理外,还需要跟2号输出的-300进行相加.
• 执行与-300相加难道直接扯根线连到2号运算器前面?
• 自然不行,(Z,374)会直接到达,此时-300还没计算出来(经过两个运算器,耗时2t).
• 根本无法完成-300+374=74这个计算
• 怎么办,等等咯.这就是D的作用.
• 保持两个信号在时间上的同步.从而正确的执行操作.
• 等来等去的那为什么不输入持续信号呢?
• 基础篇提过,持续信号本质也是脉冲信号,
• 使用持续信号,输出的结果中会有2个错误信号(因为一个信号快了2t).
• 也就是说
• 如果一个运算器需要对两个来源不同的信号进行处理(也可以是多个信号),
• 那么那两个信号需要同时到达才能完成运算,
• 这时需要使用D让两个信号同步.

• ---遵循信号同步有以下优点:
• 电路基本上全部使用脉冲信号(除了存储器部分),所有的运算器只需要对1t的信号进行处理;
• 脉冲信号也更容易进行电路的检查和调整;
• 最关键的是,它更符合人们电路设计的思路.
• 第一步做什么,然后第二步怎么处理,接着第三步什么什么....
• 缺点是电路臃肿(各种延时器),耗时长(等来等去).
• 那如果不遵循信号同步会怎么样?
• 不怎么样...
• 条条大路通罗马,
• 只不过信号同步能够简单些实现功能.
• 比如上一篇说的持续信号转脉冲信号,
• 恰恰是通过信号间的不同步实现功能(我习惯称为时差电路).
• 还有上面提到的循环电路,虽然没有取值电路和信号匹配电路好用,
• 但却是真正实现了计算2^n的电路.
• 总之依照自己的实际情况去设计电路吧.

第四部分 电路检查与暂存器

• 刚接触电路的时候,电路被我玩成了手速游戏,
• 做完电路发现有问题,
• 在确认了一遍思路后,开始逐个对运算器检查,
• 鼠标放在运算器上,眼睛盯着右边显示运算器输入与输出信号的详细信息栏.
• 等等,那个信号是啥?是不是xxx啊?详细信息里一个信号一闪而过.
• 1/60秒显然是来不及看清的,
• 让我ESC暂停看个清楚,
• 不对,按早了;不对,已经过了.再来!
• ......
• 经过不懈的努力终于成功了,电路真™难.
• 之后,看着手里的存储器,感觉宛如一个智障.

• 这里介绍一个简单但非常实用的一个小电路.

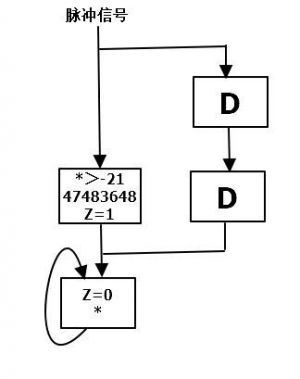
• 这是一个存储器的小改版,我称为暂存器.
• 跟存储器一样将脉冲信号转换为持续信号.
• 不同的是,暂存器在每次存储前都会先将存储器重置.
• 因此暂存器只能存储"一个"信号.
• 显而易见,这非常适合电路检查.
• 在使用存储器捕获电路中的脉冲信号,来确认电路中的信号是否正确时,
• 不得不频繁的手动重置存储器,防止信号叠加.
• 这样思路经常会被打断.
• 而暂存器就非常方便,
• 现在暂存器基本上成为我电路设计的必备工具了.
• 当然,在其他方面暂存器也有大用.
• 其功能充当了我好几个电路的主要组件.

• ---再随便说些存储器的事,
• 为了更方便电路的检查,可以对暂存器再进行改进,
• 对接收的每个脉冲信号都单独进行存储.接收多少个就存储多少个.
• 但这种只有电路检查的功能,没有实际的价值.
• 我尝试过制造这样的存储器,
• 但建到一半感觉如果你只有这样才能找到问题,是不是电路能力不行啊.
• 上一篇说到过锁存器的事,
• 相信看到这的各位厂长,造个锁存器还是很容易.
• 但怎么说呢...玩这么久还没见过必须要用锁存器的地方┑(￣Д ￣)┍
• 最后是一个高端操作——高级存储器(不知道取啥名...)
• 存在堆栈的概念,根据"指针"进行存储和读取,
• 进行扩展后,理论上还能具备数据移动复制批量删除等功能.
• 原理是存储器+信号匹配+信号筛选.
• 因为太复杂,所以能用的地方太少.
• 要是真想在工厂里造一个"电脑",没准帮助很大(充当RAM).

第五部分 随机数电路的实现

• 看到很多人在问,也不什么太难的东西,这里就详细说明一下.
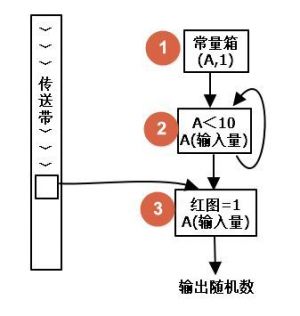
• 先制造生成一个0-9范围内的随机数的电路为例.

• 记性好的可能还记得2号运算器就是我上一篇说的"自重置计数器",
• 信号不断叠加实现计数,同时在信号达到一个值后计数器自动重置.
• 因为输入的持续信号(A,1),2号运算器的信号变化大概是这样的:
• 起始,(0),
• 第1t ,(A,1)
• 第2t, (A,2)
• 第3t ,(A,3)
• 第4t, (A,4)
• 第5t ,(A,5)
• ......
• 第8t, (A,8)
• 第9t, (A,9)
• 第10t, (0)
• 第11t, (A,1)
• 第12t, (A,2)
• 第13t, (A,3)
• ......
• 第19t, (A,9)
• 第20t, (0)
• 第21t, (A,1)
• .......
• 如此往复.不断变化.

---

• 这时你在传送带上丢一个红图,触发3号运算器,
• 3号运算器将此时2号运算器的值输出.
• 输出的这个值就是我们要的"随机数".
• 多丢几个红图,多输出几个值,你会发现输出的值是无规律的
• 因为你丢红图的时间是不确定,无规律的,
• 如果你能控制丢红图的的时间
• 比如你能精确的做到每隔0.033秒把红图丢在传送带上一个完全相同的地方.
• 那么输出的值就会呈现出每次+2的规律.
• 这就是随机数生成的逻辑---
• 在你要求生成随机数时(例子中是丢个红图),
• 电路从一个数值不断变化的运算器中取出当时的值输出.
• 这个"当时的值"取决于你要求生成随机数那个时间.
• 你无法控制你要求生成随机数的那个时间和间隔,
• 自然"当时的值"也是无法控制,无法确定,是无规律的.
• 这是伪随机,但是电路,电脑这些东西只能用伪随机,
• 它们无法做到真正的随机.
• 比较一下电脑上的随机,
• 对当前的时间(微秒级)通过一定的计算处理获得一个指定范围的数,这个数就是随机数.(也有一种随机数表的随机.)
• 可以看到电脑有一个"计算处理"的操作,所以随机数还没这么简单.

---

• 假如要获取的0-1000的随机数,那就直接把2号存储器设置为1000?
• 并不适合,这样虽然随机出来的数仍然无法精确确定,但能大致预测.
• 上一次随机出的数是354,那我马上丢个红图,下一个的值应该不会超过500,
• 最次也能肯定下一个数肯定比原来的大吧.
• 这跟随机的原则就大相径庭了.
• 可以通过让不断变化的值不那么单调来解决.
• 一个运算器的值在0-1000之间递加(A运算器),另一个运算器的值在0-10之间递加((B运算器)
• 让A运算器的值除以B运算器的值然后取余数,
• 得出一个在0-9范围随机(这里的随机指难以预测.)变动的余数.
• 把这个余数作为我们要生成的随机数的个位,
• 把电路再复制2份,让其,余数分别作为十位,百位.
• 这样整合一下就能输出一个范围在0-1000的随机数了.
• 这样足够无规律吗?
• 我不知道.
• 你可以实际造出来,拿出多个随机结果,看看是不是随机分布.
• 或者实际拿笔算一下.
• 如果把余数一个个记下来,记到一定数量肯定能发现开始与前面重复了,
• 那么多少数量会开始重复?重复周期是多少?
• 我还是不知道...
• 如果你既不想较真去计算,又不想一个个看结果,
• 那还有一个方法——凭感觉.
• 根据我小学级别的数学知识,感觉这个方法余数整体上会偏小,整和出的随机数也会偏小.

• 那就换其他方法或者改一改吧.
• 那么,到底怎么造一个能生成0-1000范围随机数的电路啊?
• 我好像什么都没说啊.
• 我可以马上造出一个电路,
• 但如果你让我说:这个电路肯定能生成0-1000范围的随机数.
• 这个太难了,我做不到,也没有那个实力和精力去证明.
• 所以我也就不说具体怎么造了,这没啥用.

---

• 之前扯了那么多,没办法,现在还有些东西要扯.
• 除了生成的随机数要求范围比较大之类的问题不好处理外,
• 要求生成多个随机数的问题更不好处理,
• 比如,丢个红图到传送带,怎么让电路输出10个随机数?
• 恩~~有个好办法,把电路复制十份,不就能一口气输出10个随机数了.
• 那怎么确保这10个相同电路输出的随机数是不相同的?
• 可以通过更改每个电路的初始条件,
• 随机电路离不开自重置计数器,让每个电路的自重置计数器的初始递加值不相同就行了.
• 当然,你的电路也需要适合这么操作.
• 还有一个问题,
• 如果一次要生成的随机数数量不确定怎么办?
• 这样不得不借助周期脉冲电路(比如环状传送带的周期脉冲)自动要求随机电路输出随机数.
• 这时候问题来了,周期脉冲,周期的,是每隔一段固定的时间去要求生成随机数的,
• 那么在这种间隔时间都固定的情况怎么保证输出的数还是无规律的?
• 延长重复周期.
• 前面说过一个在0-1000之间递加的值除以一个在0-10之间递加的值取余数,
• 其,余数一定存在一个重复周期.
• 在随机电路中,不管你的计数器再多再复杂,各种加减乘除再繁琐,
• 最后输出的随机数肯定还是有重复周期了.
• 只要保证重复周期足够长就行,或者在一段时间内不会重复也许.
• 到底怎么延长?
• 这个.....咳咳.
• 你的计数器越多越复杂,各种加减乘除越繁琐,
• 重复周期应该大概也就越长.

---

• 最后再说下贪吃蛇的随机电路大概设计过程的,以供参考.
• 首先使用了四种周期脉冲信号输出器:
• 非门脉冲;
• 环状黄带脉冲;
• 环状红带脉冲;
• 环状蓝带脉冲;
• 4种不同周期的脉冲连到两个自重置计数器上.
• 凭心情连,一个计数器大概连1~3种脉冲,有时候还会加点计数器出来(尝试了好多次,试了很多姿势)
• 一个计数器的值0-19循环递加变动,另一个计数器值0-9循环递加变动,(最初是14-14,也是试了好多次,感觉19-9不错哦)
• 两个计数器各取一个值,加一起就是一个0-28范围的随机数,
• 电路复制下,再生成一个0-28范围的随机数.
• 两个随机数一结合就是一个坐标,
• 然后检查这个坐标是否可用,不可用自动让电路重新生成.
• 可用那就是蛇要吃的"豆子"的坐标了.
• 这个随机电路合不合格?
• 我选择实际测试.
• 在那个介绍贪吃蛇的帖子我发了几张测试结果图,
• 你可以理解为是给这个电路发"合格证"......

完结

• 写教程时有种奇怪的感觉,
• 没写的时候-----有好多东西要讲,这个、那个都要说一下,还有那什么什么也要提一句.
• 写完了-----这些东西好像都说过啊,唉,这个大家明明都能想到的,等等,后面的那啥啥其实没啥卵用吧.

• 不过最后还是写完了,
• 希望对大家能有所帮助.