创世神（WorldEdit）/教程/函数生成指令分析

函数生成指令分析

教程信息

更新状态

已完结

作者

LocusAzzurro

外部链接

MCBBS原贴

“

使用表达式来生成任何你想要的东西！

”

这是一个对WorldEdit中//generate指令的研究与分析，在这里与大家分享获得的成果，一起发掘这个功能更多的潜能。

指令简介

//generate为WorldEdit中的一个指令，可简写为//gen或//g，作用是按照用户给出的一个表达式生成对应的形状。这个是WorldEdit一个非常强大的功能，理论上下可以生成任何使用表达式表示的物体，但实际使用有一个较大的限制，由于Minecraft单指令可以输入的最大字符数，过长的表达式无法输入，但就算如此，这个指令仍然可以用来完成一些复杂的操作，在Minecraft各个领域得到应用。在这里我将与各位讲解一下这个指令的使用方法，使用时的注意事项，以及我研究与找到的一些实际使用方法与例子，也希望各位如果有能力一起来完善对这个指令的研究，发掘出他更多的潜力。在正式开始之前，我们来看一个来自WorldEdit Wiki的例子来了解这个指令的强大效果。

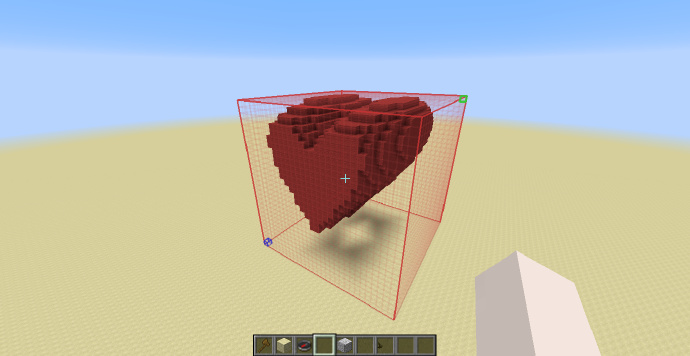
一个心形，仅使用了一个指令生成，虽然在这里我不会介绍如此复杂的使用方式，但从这里也不难看出这个指令的强大。用来生成它的指令为：

//g wool:red (z/2)^2+x^2+(5*y/4-sqrt(abs(x)))^2<0.6

接下来将会一一说明这个指令的结构与使用方式。

指令结构与使用方式

让我们来看一下之前的指令

//g wool:red (z/2)^2+x^2+(5*y/4-sqrt(abs(x)))^2<0.6

这其中//g为//generate指令的简写，wool:red为使用的方块ID，这里是红色羊毛，可以是数字ID（如1，2），可以是文字ID（如stone，grass）剩余的部分为生成使用的指令，例子中使用的是一个十分复杂的指令，因为并不是本文的重点，我们就不在这里深入研究了。

但这里要讲解一下表达式书写的方式与需要注意的地方首先让我们看一下表达式的写法，它的写法与Java相似：

• 加减乘除分别为+ - * /；
• 次方为 ^ ，这个符号在这里不表示逻辑异或门；
• 使用多重括号时仅能使用圆括号；
• 在表达式中可以使用&&来代表逻辑与门，用||来代表逻辑或门，!比较特殊，加在一段表达式前代表逻辑非门，加在表达式或数字之后代表数学阶乘(更详细的介绍见下文逻辑门部分)；
• 比较使用的是 < > (大于与小于)，<=(小于等于)，>=(大于等于)，==(等于)，!=(不等于)；
• 一般的函数是可以在表达式中使用的，如abs()绝对值，cos()正弦，sqrt()平方根等，完整的列表可以查看WorldEdit Wiki (在下文的函数部分会有更多的介绍)。

需要注意的地方有：与日常书写表达式不同，[math]\displaystyle{ 2x }[/math]，[math]\displaystyle{ 3y }[/math]等需要用乘号链接，即2*x，3*y；

最后但并不是最不重要的，WorldEdit中使用的是并不是等式，而是不等式，因为WorldEdit会将选区内的每个方块的位置带入计算，并将结果用方块反映出来，此处的结果只能是1，即有方块，或0，即无方块。如果使用等式的话，由于Minecraft为方块世界，精细度不能达到显示结果的程度，所以效果不佳。（等式无法使用的原因为笔者个人推测，如有错误请指出）但虽然不能使用等式，我们仍可以使用-h标示来达到接近的效果，这部分我们会在介绍标示时继续深入。

综上所述，这个指令的格式为：

//generate <ID> [-h/-r/-o] <表达式>

-h，-r，-o为这个指令可以使用的标示。

使用这个指令的时候需要选择一个选区，形状会在这个选择的选区中生成，注意选区的形状会影响到输出的形状，有时这个特性会造成一些麻烦，但有时可以使用这个来达到希望的效果，这一点我们接下来会讲到。

同时，就像刚才提到的，在使用这个指令时，我们可以使用一个或几个标示来改变指令的效果，来达到需要的结果。

可用标示[简介]

在使用指令时，我们可以添加一个或多个标示来改变指令的运行方式，添加标示的方法很简单，只需要将标示像添加参数一样的方式添加至指令中即可。如： //g 1 -h x>y

可用的标示有三个，分别是-h，-r与-o。

• -h 会使生成的形状空心；
• -r 会使生成时使用源坐标；
• -o 会使生成时使用源坐标，同时将坐标系原点移动到玩家位置（或者玩家的第一选择点，如果使用了/toggleplace）。

-r 与 -o 的效果冲突，因此-o的效果会覆盖掉-r的效果。-h 与 -r 或 -o二者之一可以同时使用。 这里仅仅给出一个标示的基本介绍，在本文之后的章节中会一一介绍它们的效果，接下来我们首先来集中看一下不使用任何标示的情况。

坐标范围

在不使用任何标示的情况下，WorldEdit会将当前的选区看做一个三维直角坐标系，坐标系原点为选区中心。

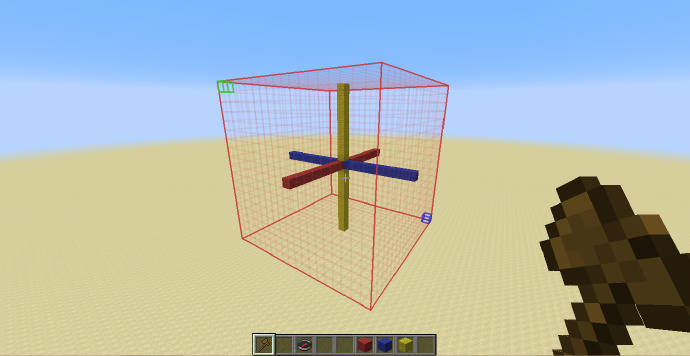
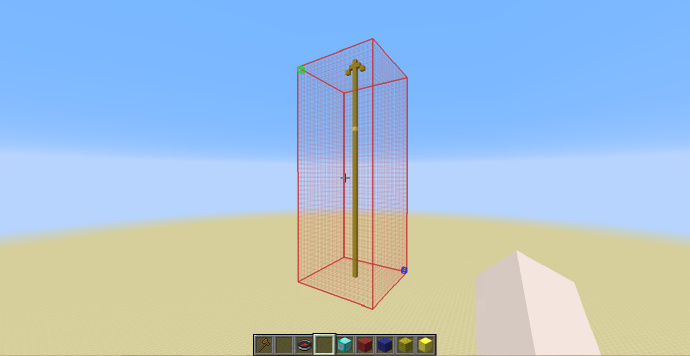
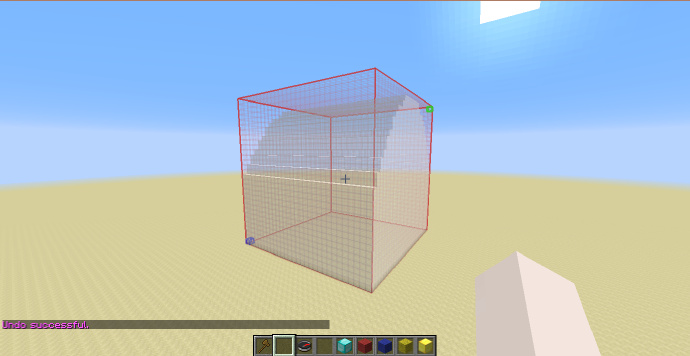
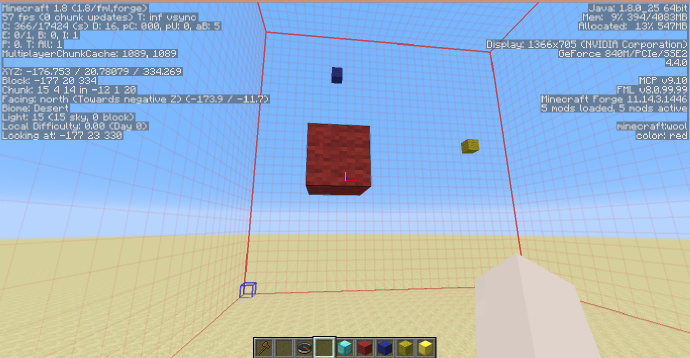
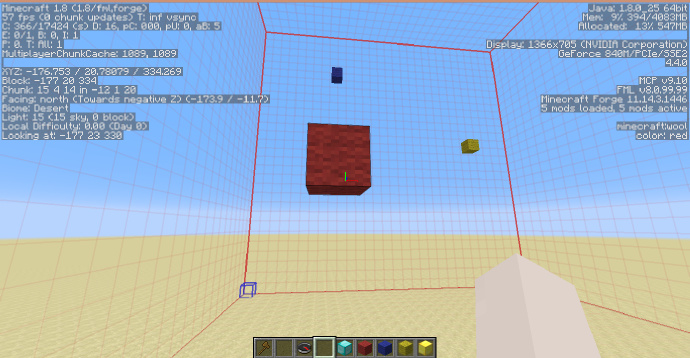
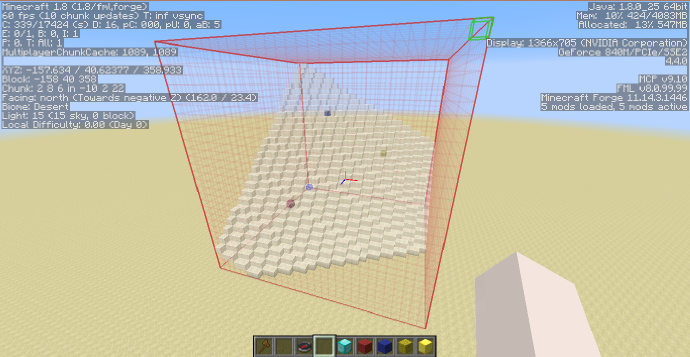
如图，我用羊毛标出了三条坐标轴，WorldEdit使用的坐标轴系统与Minecraft的相同，即从西(负)到东(正)为[math]\displaystyle{ X }[/math]轴(蓝)，从下到上为[math]\displaystyle{ Y }[/math]轴(黄)，从北到南为[math]\displaystyle{ Z }[/math]轴(红)。 这个坐标系三条轴的界限为[math]\displaystyle{ -1 }[/math]与[math]\displaystyle{ +1 }[/math]，也可以说生成的范围为[math]\displaystyle{ [-1;+1] }[/math]，注意这个界限仅在不使用标示或仅使用-h标示时存在，-r 与 -o 的运行方式完全不同，我们在下文会分别看到他们的生成方式。

如上图，我在坐标轴上用金块与钻石块标出了两个点，按照刚才我们讲到的，金块的坐标应为[math]\displaystyle{ (0;0.5;5) }[/math]，即[math]\displaystyle{ Y }[/math]值为[math]\displaystyle{ 0.5 }[/math]，钻石块的坐标为[math]\displaystyle{ (0.5;0;0) }[/math]即[math]\displaystyle{ X }[/math]值为[math]\displaystyle{ 0.5 }[/math]。 下面我们来试试使用几个简单的方程。

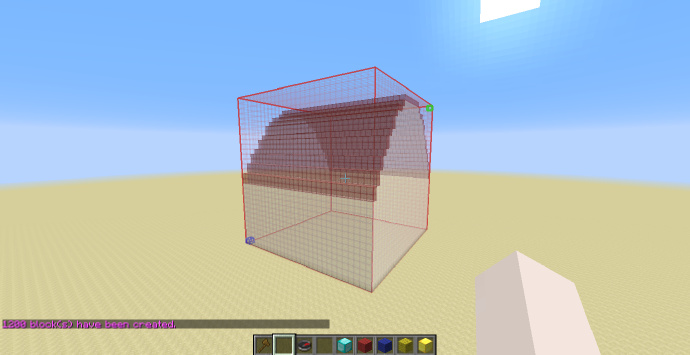
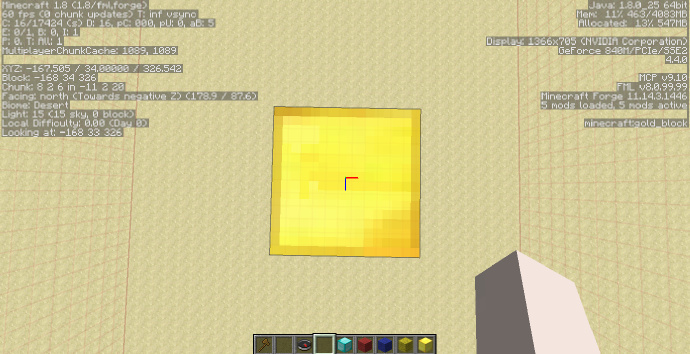
上图使用的是：

//g 95:0 y<0.5

效果即为将所有Y值小于0.5的方块位置设置为白色玻璃方块。

接下来我们来试试曲面。

这里使用了球体的公式：

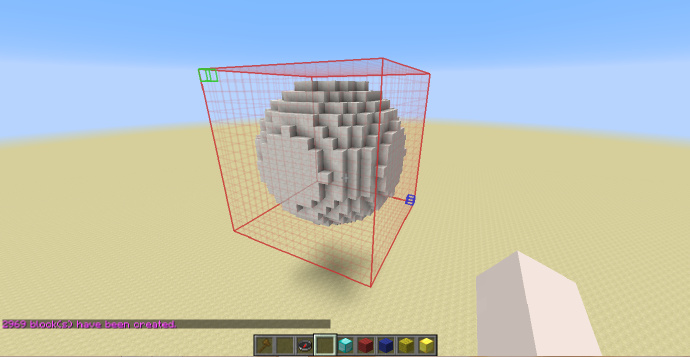
//g 155 x^2+y^2+z^2<1

生成出的就是半径为[math]\displaystyle{ 1 }[/math]的实心球体（如果你说这个球半径不是1建议重新阅读本章节）。

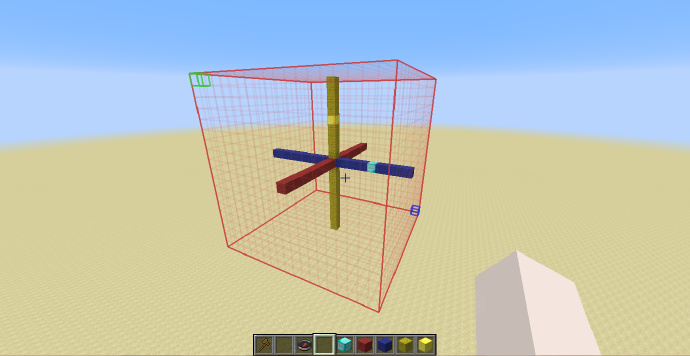
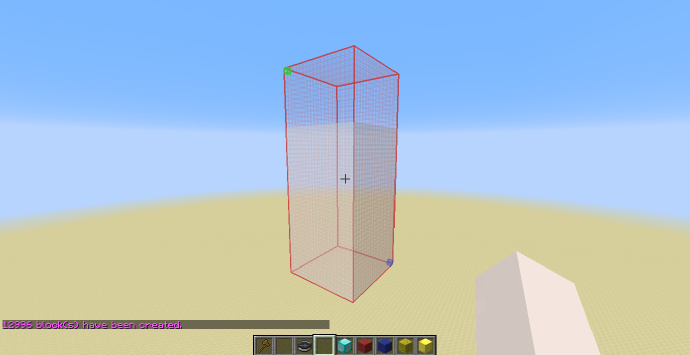
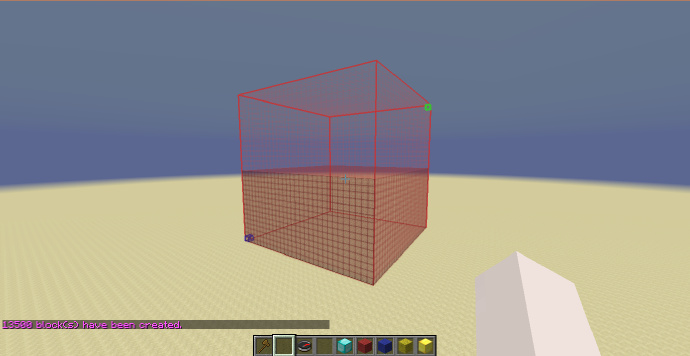
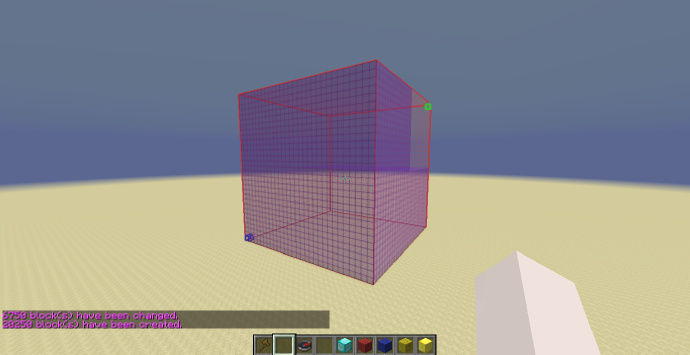
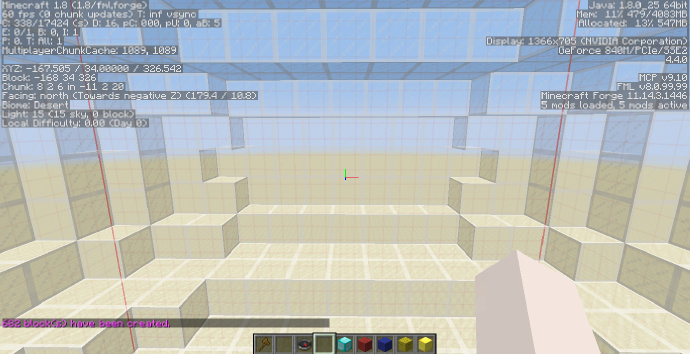
到这里可能各位都注意到了（什么？你说你没有？），这几次生成使用的选区都是一个正方体，这是因为只有这样生成出的形体才是比例正确的。那么如果选区不是正方体就不能生成了么？并不是，如果用来生成的选区不是正方体，生成的形状会被按照三轴之间的比例在三轴方向被拉伸或压缩，这还是因为选区的范围为从[math]\displaystyle{ -1 }[/math]到[math]\displaystyle{ +1 }[/math]造成的。那么如果我用一个长方体的选区生成就是异端了么？也并不是，这两种方式各有他们的用处，如需要生成一个比例正确的结构，像是一个球体，那么使用正方体选区就是正确的选择，如果要生成的是一个椭球，则可以直接选择一个长方体选区，这样球体就会被按照比例自动被拉伸成椭球，也省去了计算椭球表达式的麻烦。 如下图，选区的Y轴实际长度为[math]\displaystyle{ X }[/math]轴和[math]\displaystyle{ Z }[/math]轴的两倍，图中的金块的坐标依然为[math]\displaystyle{ (0;0.5;0) }[/math]，在这个情况下生成的形状在[math]\displaystyle{ Y }[/math]轴上就会被拉伸两倍。

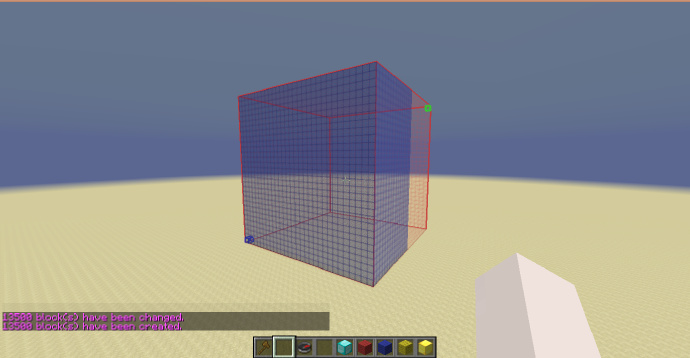
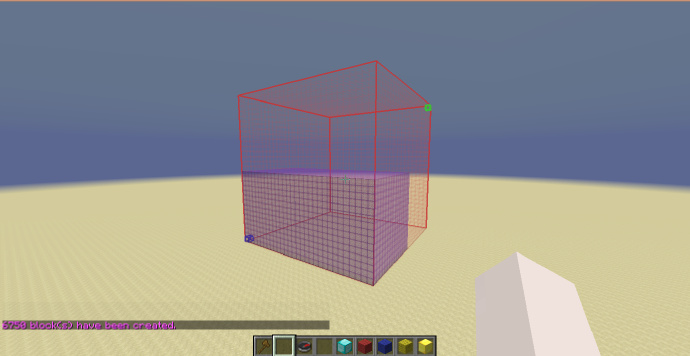
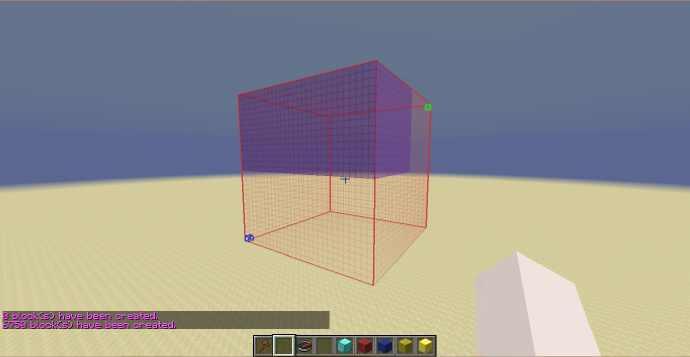
如果我们再次使用之前的：

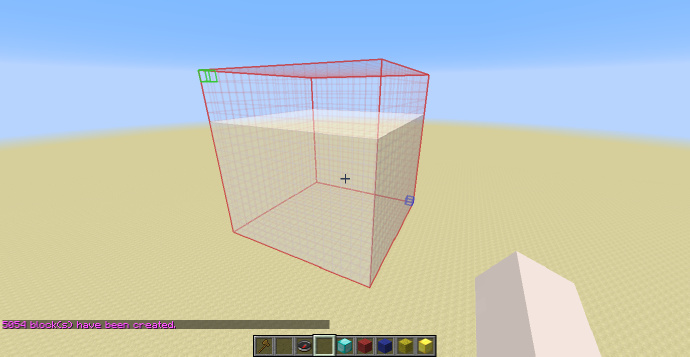
//g 95:0 y<0.5

可以看到填充的部分依然是选区下方的[math]\displaystyle{ \frac{3}{4} }[/math]部分，但在[math]\displaystyle{ Y }[/math]轴上填充的高度变为了之前的2倍。

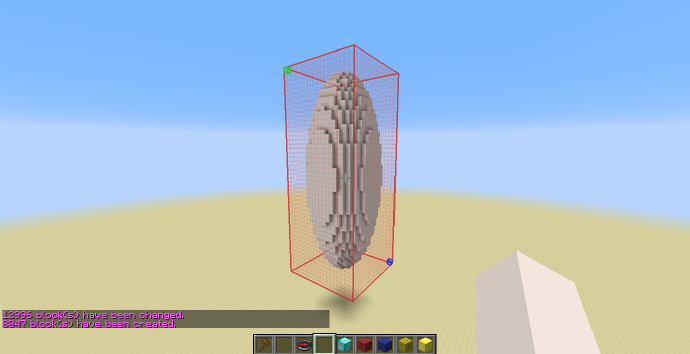
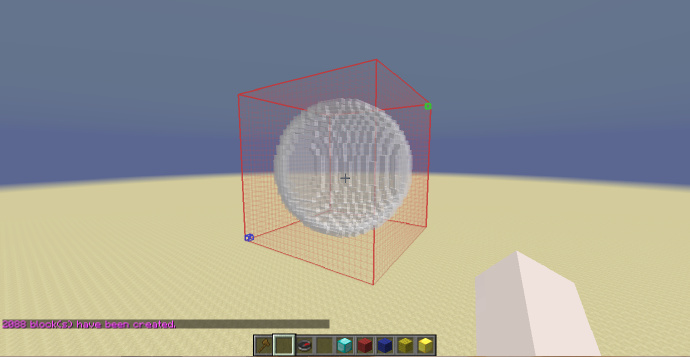
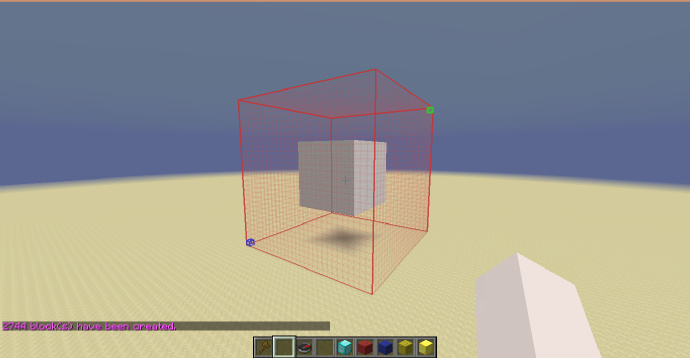
最后让我们再次使用一下之前的球体公式：

可以看到，就如刚才所说，生成出的是一个椭球。

等式与不等式

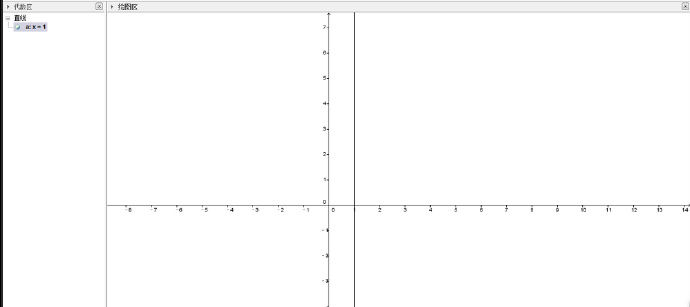
刚才提到了WorldEdit使用的不等式而非等式，这里简单来讲解一下二者的区别(学霸可以跳过)。 下面的这个等式是一条直线：

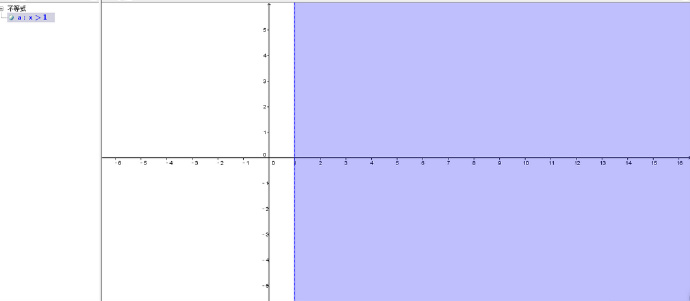
而不等式表达的是一个区域：

WorldEdit中使用的是不等式，来表达一个区域，这个区域中的方块位置便会被放置方块。

空心图形标示的使用

刚才我们提到了生成时可以使用标示来改变命令的输出，首先我们来看一下空心图形标示，即-h ，它的作用是可以使生成的图形“空心”，即只有图形边缘位置的方块会被生成，这个边缘的判定方式是“如果这个方块位置一方块单位周围的任何方块位置不属于这个图形，那么这个位置的方块就会被生成，反之则不生成。”

首先我们来看一个例子：

上图使用的指令是：

//g 95:0 x^2+y<1

即一个抛物面的下方部分。

如果使用相同的表达式，但是使用-h标示，结果就会是这样的（下图红色玻璃部分为新指令输出，覆盖到白色玻璃的旧指令的输出上进行比较）。

可以看到，只有抛物面最上方（也可以说只有抛物面本身）的位置生成了方块。上图使用的是//g 95:14 -h x^2+y<1。

就像我们刚刚看到的，使用这个方式也可以使不等式拥有类似等式的输出，接下来我们来看一下另一个例子。在本文开始的部分我们提到了球体内部的不等式x^2+y^2+z^2<1。

如果我们使用-h标示，就可以生成空心的球体，即表达式为x^2+y^2+z^2=1的球面，虽然并不能达到完全准确，但也能达到一部分。

那么，我们来看一下生成的效果：

上图使用的命令为：

//g 95:0 -h x^2+y^2+z^2<1

可以看到使用空心图形标示的效果。

到现在为止，我们使用的例子都是简单的平面或曲面，那么各位可能会问了，像是正方体这种有棱有角的多面体可以生成吗？答案是肯定的，但生成多面体我们需要用到另一个功能，那就是逻辑门。

使用空心标示的原因

虽然这里说了可以使用-h标示来模拟等式的效果，但是其实WorldEdit的函数处理器也支持相等==的计算。但是使用==运算符大部分情况下并不能达到我们期望的效果。

这个问题在不使用真实坐标-r及-o标识的情况下最为明显，这里就用这个模式进行演示。根据前文我们知道，在不使用真实坐标时，选区会被标准化为[math]\displaystyle{ [-1;+1] }[/math]之间的空间。在正常的[math]\displaystyle{ R^3 }[/math]空间中，这个区间是连续的，其中有无数个点。但Minecraft中每个方块的坐标只能是整数，所有方块的坐标的集合可以视作[math]\displaystyle{ Z^3 }[/math]的子集。因此，在进行函数结构生成时，选区里的每个方块的位置都会被转化为[math]\displaystyle{ [-1;+1] }[/math]中的一个坐标来参与之后的计算，而选区中的方块数量是有限的，这里得到的坐标数量也是有限的。另一方面，WorldEdit的函数处理器（基于Java机制）中的==运算符只有当表达式两边的值完全相等时才会返回1（true），放到这里就是生成函数结构的方块。因此，把这两个原因结合起来，如果我们在进行函数结构生成时使用==运算符，只有在某个方块的坐标转换出的标准化坐标刚好完全（或者几乎完全）满足等式的情况下，这个坐标上才会生成方块。

如下图为使用//gen 41 x^2+y^2+z^2==1进行生成的结果，可以看到只有少量方块被成功生成。

逻辑门的使用与多面体

在之前我们提到了在表达式中可以使用逻辑门，我们首先来回顾一下：

• && 表示逻辑与门；
• || 表示逻辑或门；
• ! 加在一段表达式前表示逻辑非门。

那么这些逻辑门有什么作用呢，我们来一个个看一下：

逻辑与门代表集合论中的交集，即同时属于两个或更多集合的元素，在几何中我们可以理解为同时满足多个不等式的部分。

我们可以用一个例子来理解一下：

如下图表示的是[math]\displaystyle{ y\lt 0 }[/math]的区域指令：

//g 95:14 y<0

下图表示的是[math]\displaystyle{ x\lt 0 }[/math]的区域指令：

//g 95:11 x<0

那么如果我们使用逻辑与门将两个表达式连接，即y<0 && x<0，我们表达的是两部分的交集（即[math]\displaystyle{ y\lt 0\cap x\lt 0 }[/math]），即同时满足两个不等式的区域，也可以说是两部分共有的区域。使用指令：

//g 95:10 y<0 && x<0

我们会得到下面的结果：

这印证了我们刚才所说的，只有两部分（红色与蓝色的部分）共有的区域被生成了。

接下来是逻辑或门，它相当于集合论中的并集，如果我们依旧使用之前的两个不等式x<0与y<0但使用逻辑与门来连接，即x<0 || y<0，我们表达的是两个不等式的并集[math]\displaystyle{ (x\lt 0\cup y\lt 0) }[/math]，即两个不等式的区域相加的结果，也可以说是所有包括在两个不等式的任何一个中或两个中的区域。使用指令：

//g 95:10 y<0 || x<0

我们得到的是下面的结果：

可以看到，生成的区域包括了之前两个不等式所有的部分。

最后我们一起看一下逻辑非门以及多个逻辑门的使用。逻辑非门表示“不属于这个集合的部分”，即如果我们的集合是[math]\displaystyle{ y\lt 0 }[/math]，那么如果我们在它之前加上非门，即 !(y<0) （由于!符号的多种意义，建议在为需要使用非门的部分加上括号），我们表达的就是[math]\displaystyle{ y\gt 0 }[/math] 的部分（其实是[math]\displaystyle{ y\ge 0 }[/math]，但WorldEdit不支持等式），即不属于[math]\displaystyle{ y\lt 0 }[/math]的部分。多个逻辑门的使用即为使用多个逻辑门来表达一个特定的区域，这里需要注意的是，就像数学计算一样，先乘除后加减，先计算括号内部分，从左到右计算一样，逻辑运算也有它的规则：

• 三个逻辑运算的优先级为：非门 > 与门 > 或门
• 和数学运算一样，逻辑运算中括号也有最高的优先级，并遵循从左到右的运算顺序。

同样，我们继续使用之前的两个不等式来举例，这一次我们表达的是：

x<0 && !(y<0)

表达的是[math]\displaystyle{ x\lt 0 }[/math]与非[math]\displaystyle{ y\lt 0 }[/math]的交集，我们知道我们首先需要计算非门，所以我们的表达式可以理解为：

x<0 && y>0

即为[math]\displaystyle{ x\lt 0 }[/math]与[math]\displaystyle{ y\gt 0 }[/math]的交集。整个表达式表达的是“x>0区域与非y<0区域共有的部分”。让我们把它写进命令里：

//g 95:10 x<0 && !(y<0)

会得到这个结果：

就像我们刚才所说。

讲了那么多我们来看一个实际的例子，一个在选区中心，边长为1的正方体，我们需要先确定正方体6个面所属的平面，然后用不等式决定区域（这里需要有些3D分析能力），找到6个不等式然后将它们用逻辑与门&&连起来，意思就是找到这6个区域共有的区域，那个区域就是我们的正方体了。

我们的正方体的8个顶点分别为：

• [math]\displaystyle{ (0.5;0.5;0.5) }[/math]
• [math]\displaystyle{ (0.5;-0.5;0.5) }[/math]
• [math]\displaystyle{ (0.5;0.5;-0.5) }[/math]
• [math]\displaystyle{ (0.5;-0.5;-0.5) }[/math]
• [math]\displaystyle{ (-0.5;0.5;0.5) }[/math]
• [math]\displaystyle{ (-0.5;-0.5;0.5) }[/math]
• [math]\displaystyle{ (-0.5;0.5;-0.5) }[/math]
• [math]\displaystyle{ (-0.5;-0.5;-0.5) }[/math]

它的六个面所属的六个平面将会分别为：

• [math]\displaystyle{ x=0.5 }[/math]
• [math]\displaystyle{ x=-0.5 }[/math]
• [math]\displaystyle{ y=0.5 }[/math]
• [math]\displaystyle{ y=-0.5 }[/math]
• [math]\displaystyle{ z=0.5 }[/math]
• [math]\displaystyle{ z=-0.5 }[/math]

接下来将它们变为不等式：

• [math]\displaystyle{ x\lt 0.5 }[/math]
• [math]\displaystyle{ x\gt -0.5 }[/math]
• [math]\displaystyle{ y\lt 0.5 }[/math]
• [math]\displaystyle{ y\gt -0.5 }[/math]
• [math]\displaystyle{ z\lt 0.5 }[/math]
• [math]\displaystyle{ z\gt -0.5 }[/math]

这6个不等式的空间区域的交集就是那个正方体了。我们用&&表示逻辑与门，就是交集，这样就可以把6个不等式连起来：

x<0.5 && x>-0.5 && y<0.5 && y>-0.5 && z<0.5 && z>-0.5

最后的指令就是：

//g 155 x<0.5 && x>-0.5 && y<0.5 && y>-0.5 && z<0.5 && z>-0.5

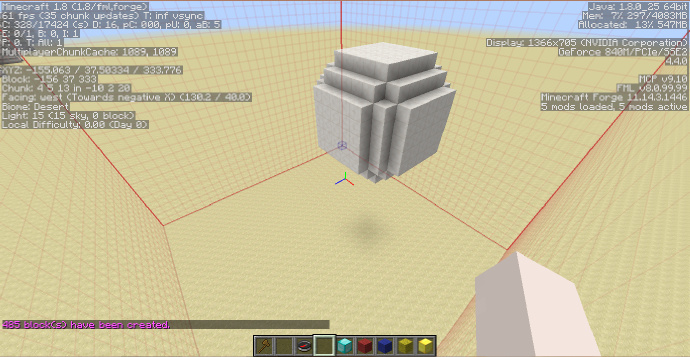
输入指令，成功生成了正方体：

以上便是多面体的生成方式以及逻辑门的使用，接下来我们来通过几个例子看一看WorldEdit中函数的使用。

函数的使用

在表达式中我们可以使用一系列的函数，使用的方法与日常的写法相似，即函数(<输入值>)，这里我们来使用几个常见的函数作为例子了解一下它们在表达式中的应用。

上图使用了：

//g 155 y<abs(x)

其中abs(x)代表的便是[math]\displaystyle{ x }[/math]的绝对值。

下面这个是正弦[math]\displaystyle{ \sin{x} }[/math]，同时使用了-h来仅生成正弦的曲线（什么？你想说说好的曲线呢？有两种可能，一是你没仔细看前面的，二是你三角函数没学好）。

上图使用的指令是：

//g 95:0 sin(x)<y

那么为了更容易得看出曲线，我们可以对它进行一些压缩：

这里我们使用了：

//g 95:0 sin(4*x)<y

这样就能明显看出正弦的曲线了。

除了提到的这两个，生成时还可以使用许多其他的函数，各位可以参考前文给出的链接中的列表来了解。

接下来，我们将会讲解生成时可以使用的另外两个标示，-r 与 -o 这两个标示的运作方式与之前提到的完全不同。

源坐标的使用

现在我们来关注一下-r 标示，它的作用是使生成时使用源坐标，简单来说，就是将整个地图视作一个巨大的立体直角坐标系，虽然生成的范围依旧会被限制在选区中，但使用指令时可以带入实际的坐标进行（即F3画面上的[math]\displaystyle{ X Y Z }[/math]坐标）运算。

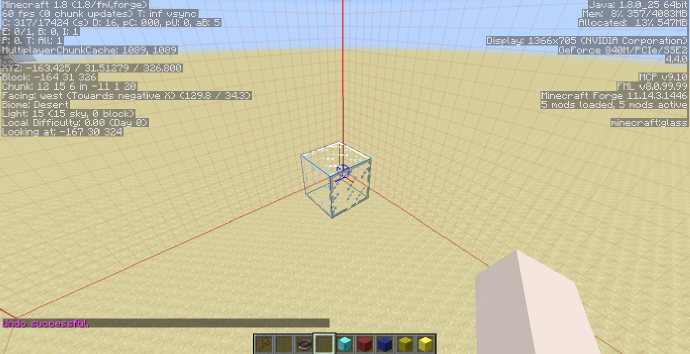
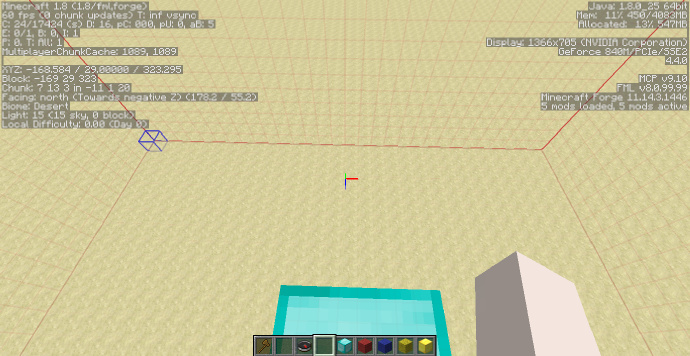
这样说起来可能不好理解，让我们来看一个例子吧：

我们的目标是建立一个以上图的玻璃方块位置为中心，半径为5的球体，首先我们需要得到这个玻璃方块的坐标，即[math]\displaystyle{ (-167;30;324) }[/math]（见上图左上角最后一行Looking at:）。 我们知道，三维球面的方程是 [math]\displaystyle{ (x-x_c)^2 + (y-y_c)^2 + (z-z_c)^2 = r^2 }[/math]。

带入我们的中心点坐标，并加上半径5，就成了：

[math]\displaystyle{ (x+167)^2+(y-30)^2+(z-324)^2=25 }[/math]

现在我们可以将它转化成不等式，来表达球体内部：

[math]\displaystyle{ (x+167)^2+(y-30)^2+(z-324)^2\lt 25 }[/math]

将其带入指令（不要忘记-r标示）：

//g 155 -r (x+167)^2+(y-30)^2+(z-324)^2<25

输入指令，可以得到下面的结果：

我们成功地在正确的位置生成了正确的球体（你说你弄这么一大堆就为跟我说个球？） 接着我们来看这个模式可能的另一个应用，使用三个点来生成一个平面：

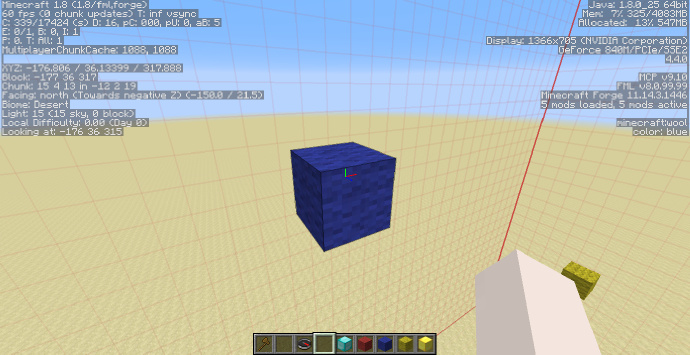
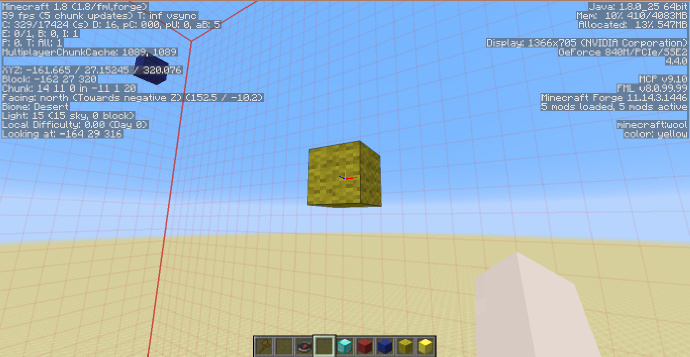
如上图，在空间里选择了三个点，使用羊毛标注，我们的目标是找到并生成这过这三个点的唯一平面（给出空间中三个不在同一直线的点，仅存在一个过这三点的平面）。 首先我们需要找到这三个点的坐标：

• [math]\displaystyle{ R(-177;23;230) }[/math]
• [math]\displaystyle{ B(-176;36;315) }[/math]
• [math]\displaystyle{ Y(-164;29;316) }[/math]

通过计算，我们可以得到平面的方程为：

[math]\displaystyle{ -92x-181y-163z+41669=0 }[/math]

接下来我们来将它带入指令：

//g 95:0 -r -h -92*x-181*y-163*z+41669<0

可以看到等式转换成了不等式，并且使用了-h标示来仅生成平面，输入后我们得到的是：

可以看到我们成功生成了过三点的平面，可以注意到只有这个平面在选区中的部分被生成了，也可以理解为生成了平面与选区范围的交集。

移动后源坐标的使用

最后，我们来看一下-o 标示，移动过的源坐标，它与之前的-r标示十分相似，也是使用实际地图坐标长度来进行运算，但二者的区别是-r完完全全使用的是真实的方块坐标，但-o模式会将玩家使用命令时所在的位置（或者玩家的第一个选择点，如果使用了/toggleplace），作为三维直角坐标系的原点。

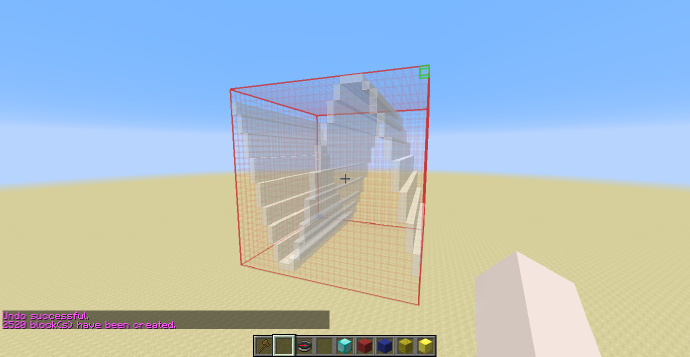
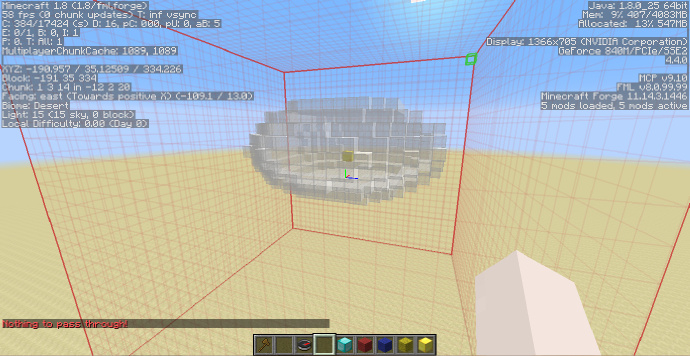
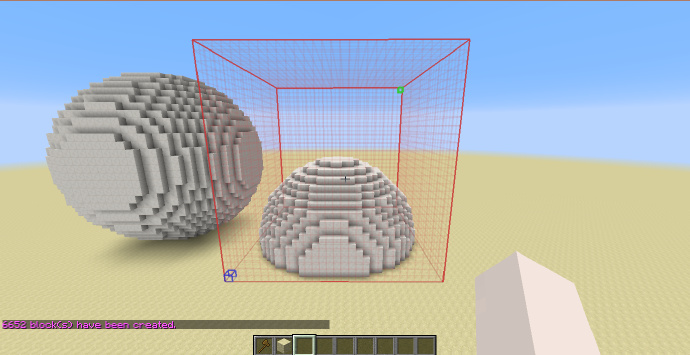
和刚才一样，我们来看一个例子：

这次我们的目标是生成一个以这个金块为中心的空心椭球，和刚才不同，我们不需要得到这个金块的坐标，而是将这个金块位置的坐标看做原点，即[math]\displaystyle{ (0;0;0) }[/math]。

接着，我们在这个位置使用指令：

//g 95:0 -o -h x^2+(2*y)^2+z^2<100

可以看到使用了-o与-h标示，并且并没有对像刚才一样带入中心点的坐标，如此输入的结果是：

从外面看的效果如下：

成功生成了需要的椭球。

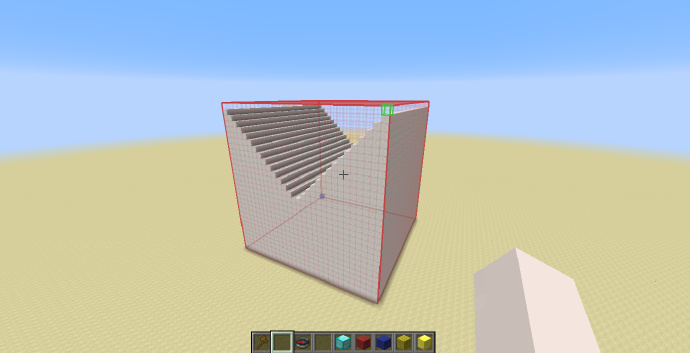
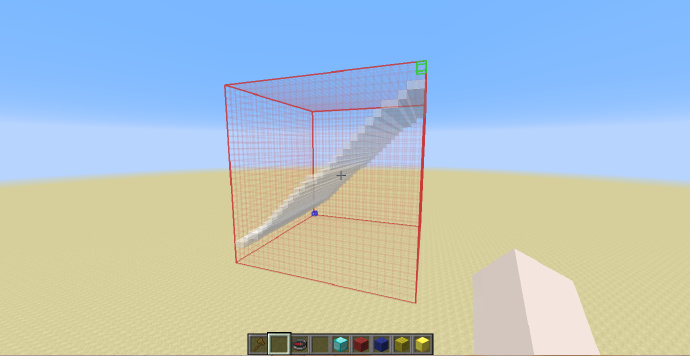
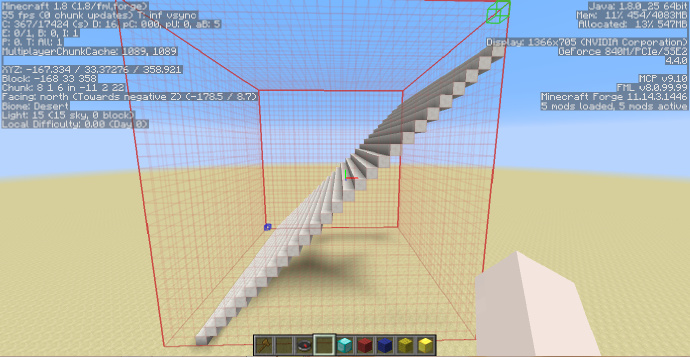
最后我们来看一个斜面：

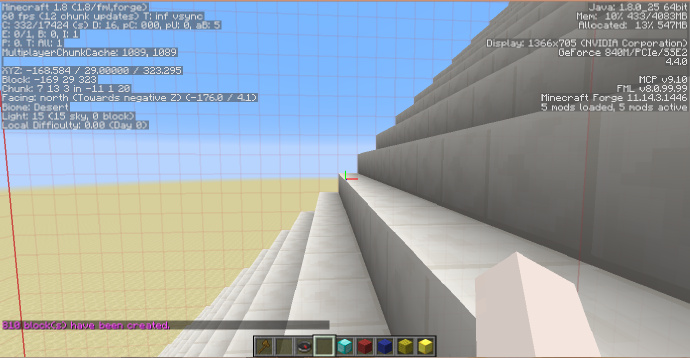
如上图，我们在钻石块位置使用指令：

//g 155 -o -h x<y

因为[math]\displaystyle{ x=y }[/math]平面的特性，可以生成一个45度的斜面效果如下：

整体效果：

至此，对于指令本身的研究结束，接下来会展示一些本人收集到的一些实际的应用与实际操作例子（部分为个人研究，部分为在他人的研究之上进行的深入，部分为他人的研究）。

例子

接下来我们来了解一些这个指令的实际应用，这些应用一般与建筑有关，也会有一些其他非相关的形体。每个图形我仅会给出所用的公式与标示，前面的主命令与方块部分需要自己补全，即使用时要使用如下格式：

//g <方块ID> <下文给出部分>

另外，每种形体也提供了对应的生成出的形体的高度信息。

• [math]\displaystyle{ H_{sel} }[/math] 代表选区高度。
• [math]\displaystyle{ H_{shp} }[/math] 代表形体高度。

曲面

半球

x^2+(y+1)^2+z^2<1

[math]\displaystyle{ H_{shp}=\frac{H_{sel}}{2} }[/math]

如果使用了-h标示便可以生成半球穹顶。

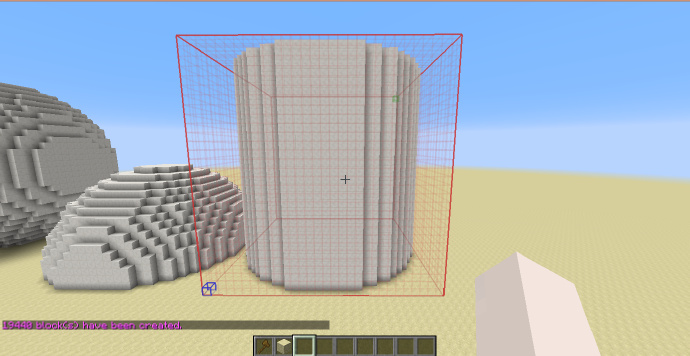
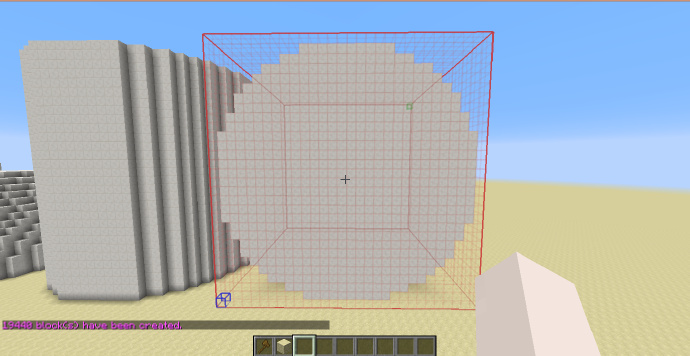
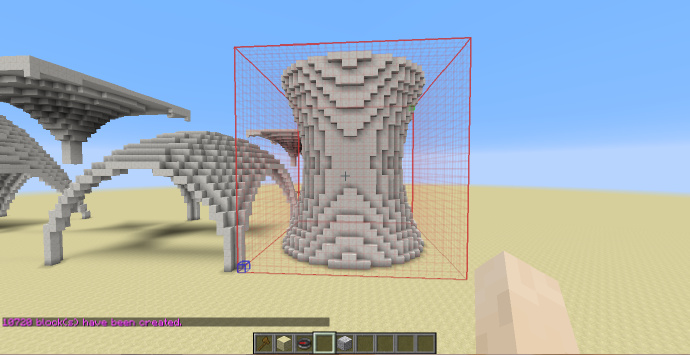
圆柱体

两个的表达式分别为：

x^2+z^2<1

x^2+y^2<1

[math]\displaystyle{ H_{shp}=H_{sel} }[/math]

使用-h可以生成空心圆柱。

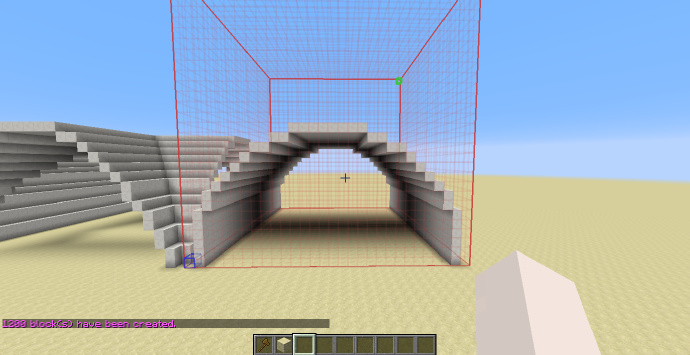
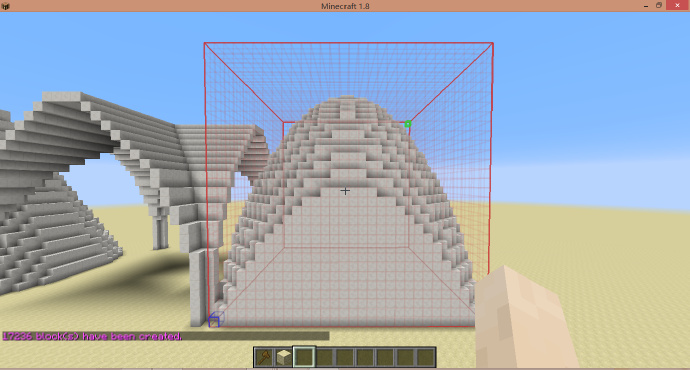
半圆拱顶

通过将上一个圆柱体向下移动一单位并使用-h得到：

-h x^2+(y+1)^2<1

[math]\displaystyle{ H_{shp}=\frac{H_{sel}}{2} }[/math]

将[math]\displaystyle{ x }[/math]替换为[math]\displaystyle{ z }[/math]可以得到另一个方向的拱顶。

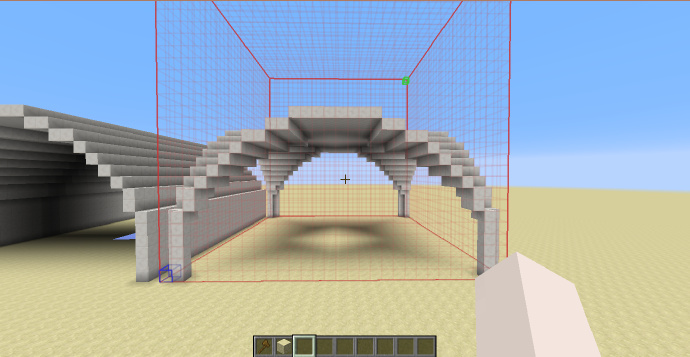
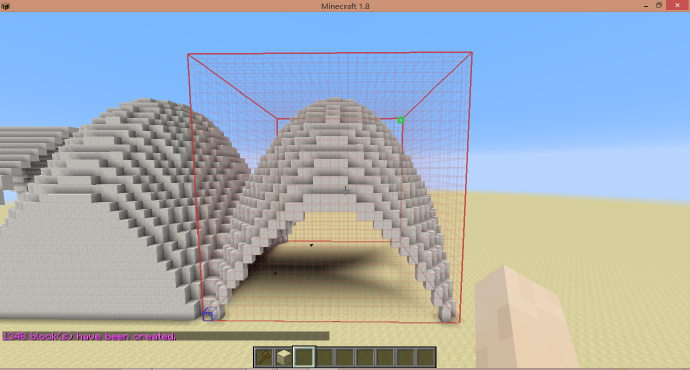
半圆十字拱/穹形拱顶

通过将两个方向的半圆拱顶交叉形成。

-h x^2+(y+1)^2<1||z^2+(y+1)^2<1

[math]\displaystyle{ H_{shp}=\frac{H_{sel}}{2} }[/math]

抛物面

-h x^2+y<0

[math]\displaystyle{ H_{shp}=\frac{H_{sel}}{2} }[/math]

将x替换为z可以生成另一方向的抛物面抛物线形的拱顶。

抛物面十字拱

通过将两个方向的抛物面交叉形成。

-h x^2+y<0||z^2+y<0

[math]\displaystyle{ H_{shp}=\frac{H_{sel}}{2} }[/math]

等角拱

通过两个稍大平移过的圆柱体的交集形成。

-h (x+1)^2+(y+1)^2<4&&(x-1)^2+(y+1)^2<4

[math]\displaystyle{ H_{shp}=\frac{\sqrt{3}}{2}\cdot H_{sel} }[/math]

将[math]\displaystyle{ x }[/math]替换为[math]\displaystyle{ z }[/math]可以生成另一个方向的拱顶。

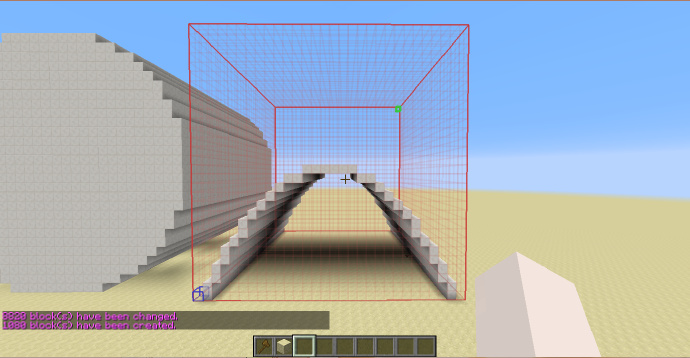
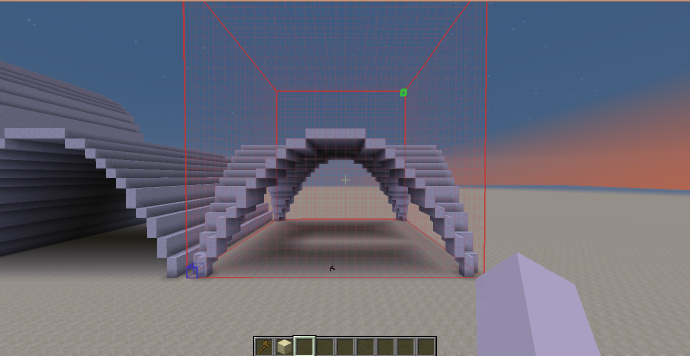
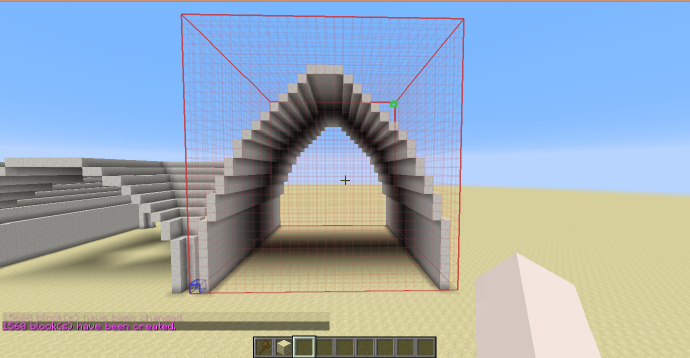
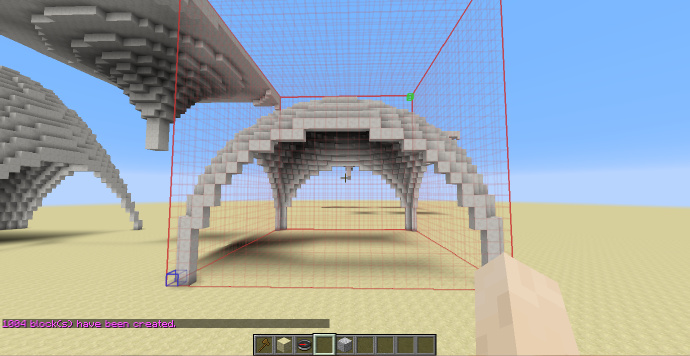
十字尖拱/肋形拱顶

通过将两个方向的等角拱交叉形成。

-h ((x+1)^2+(y+1)^2<4&&(x-1)^2+(y+1)^2<4)||((z+1)^2+(y+1)^2<4&&(z-1)^2+(y+1)^2<4)

[math]\displaystyle{ H_{shp}=\frac{\sqrt{3}}{2}\cdot H_{sel} }[/math]

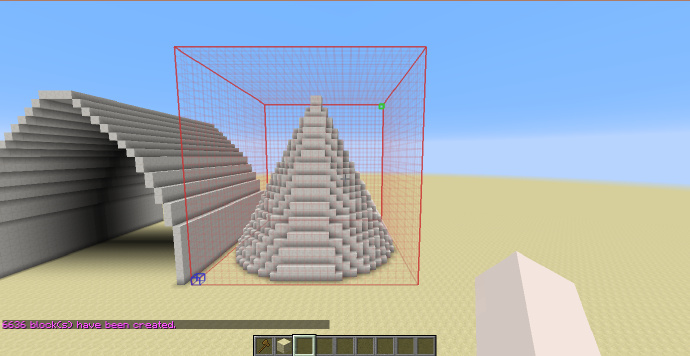
圆锥

x^2+z^2<(0.5*(y-1))^2

[math]\displaystyle{ H_{shp}=H_{sel} }[/math]

使用-h可以生成空心形体。

旋转抛物面

x^2+z^2+y<1

[math]\displaystyle{ H_{shp}=H_{sel} }[/math]

抛物面帆拱

通过上一个形体的空心形体得到。

x^2+z^2+y<1

[math]\displaystyle{ H_{shp}=H_{sel} }[/math]

帆拱为从圆形面到方形面的转换。

球形帆拱

通过稍大的半球穹顶的空心形体得到。

-h x^2+(y+1)^2+z^2<2

[math]\displaystyle{ H_{shp}=H_{sel} }[/math]

双曲面

x^2/A+z^2/B-y^2/C<D

[math]\displaystyle{ A,B,C,D }[/math]可以分别取值，下图使用的是：

x^2/0.4+z^2/0.4-y^2<1

[math]\displaystyle{ H_{shp}=H_{sel} }[/math]

圆弧旋转面

通过将圆弧沿[math]\displaystyle{ Y }[/math]轴旋转一周得到：

(1-sqrt(x^2+z^2))^2+y^2 > A && y>0

[math]\displaystyle{ A }[/math]可取值来决定大小，下图使用：

(1-sqrt(x^2+z^2))^2+y^2 > 0.9 && y>0

[math]\displaystyle{ H_{shp}=\frac{H_{sel}}{2} }[/math]

生成在选区上半部分将多个形体连续放置可以得到扇形拱顶。

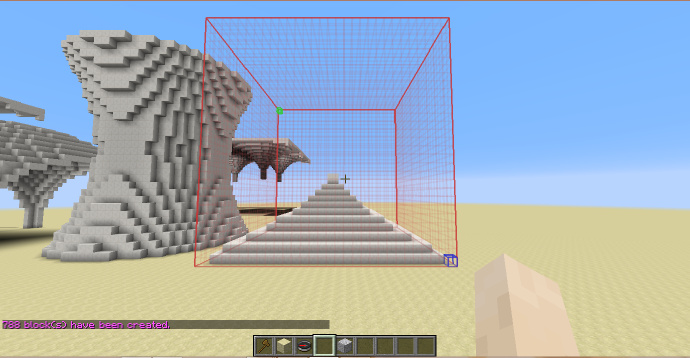
四面攒尖顶

通过四个方向的抛物面外部的交集形成，并只取下半部分。

-h y^2+x>0&&y^2+z>0&&y^2-x>0&&y^2-z>0&&y<0

[math]\displaystyle{ H_{shp}=\frac{H_{sel}}{2} }[/math]

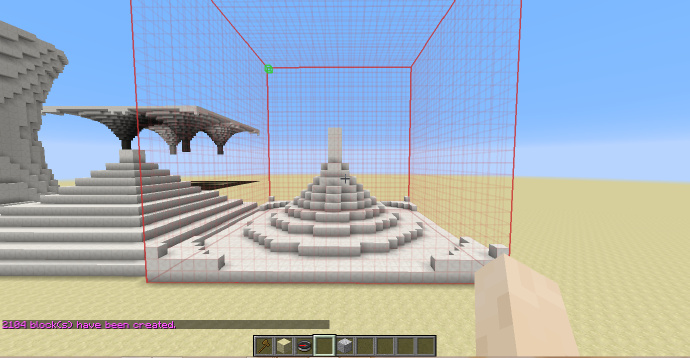
圆形攒尖顶

圆弧旋转面的下半边。

(1-sqrt(x^2+z^2))^2+y^2 > A && y<0

[math]\displaystyle{ A }[/math]可取值决定大小，下图使用：

(1-sqrt(x^2+z^2))^2+y^2 > 0.9 && y<0

[math]\displaystyle{ H_{shp}=\frac{H_{sel}}{2} }[/math]

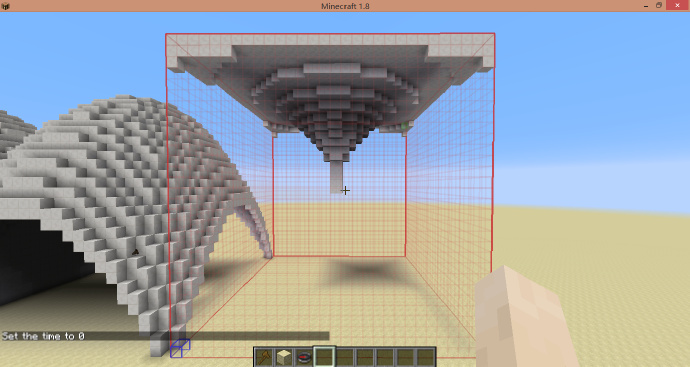
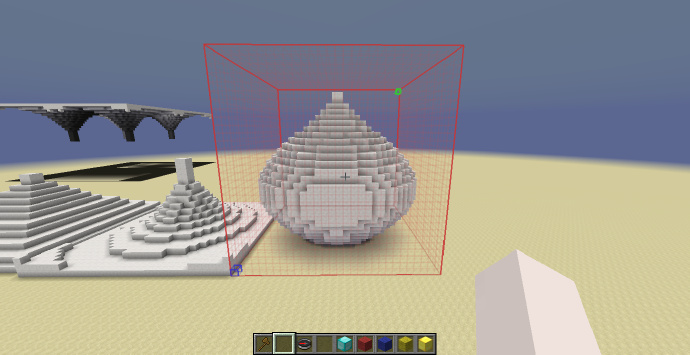
葱型圆顶

-h x^2+z^2<(0.5*sin(0.75*pi*(y+1))+0.5)^2

[math]\displaystyle{ H_{shp}=H_{sel} }[/math]

多面体

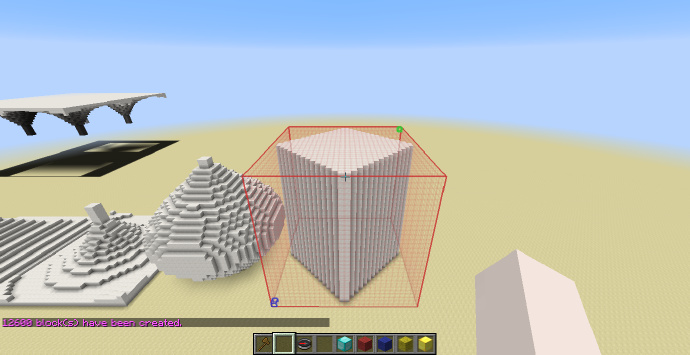
四棱柱

旋转[math]\displaystyle{ 45^\circ }[/math]后的正方体。

-2*x+2*z+2>0 && -2*x-2*z+2>0 && 2*x+2*z+2>0 && 2*x-2*z+2>0

[math]\displaystyle{ H_{shp}=H_{sel} }[/math]

三棱柱

底边平行于[math]\displaystyle{ X }[/math]轴。

z<(3*sqrt(2)/2)*x+(3*sqrt(2)-2)/2 && z<-(3*sqrt(2)/2)*x+(3*sqrt(2)-2)/2

[math]\displaystyle{ H_{shp}=H_{sel} }[/math]

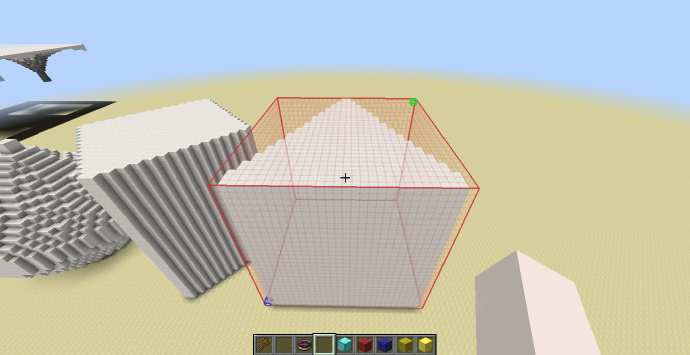
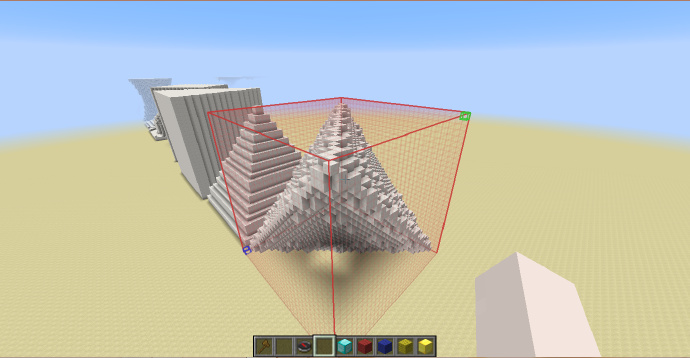
金字塔/四棱锥

-2*x-y+1>0 && 2*x-y+1>0 && -2*z-y+1>0 && 2*z-y+1>0

[math]\displaystyle{ H_{shp}=H_{sel} }[/math]

四面体

4*x + 4*y +4*z + 4>0 &&-4*x + 4*y +4*z -4<0&&-4*x + 4*y +-4*z + 4>0&&4*x + 4*y +-4*z -4<0

[math]\displaystyle{ H_{shp}=H_{sel} }[/math]

使用例子

最后，我们来看几个实际的操作例子：

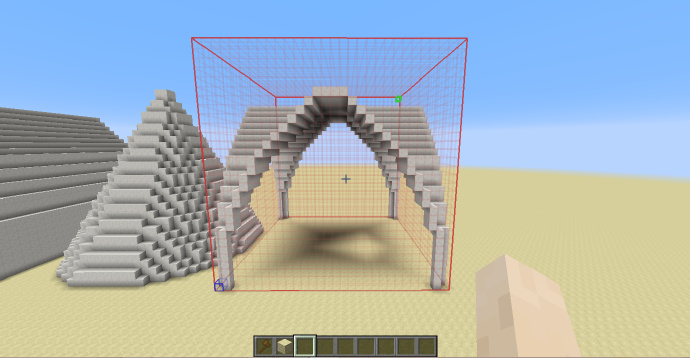
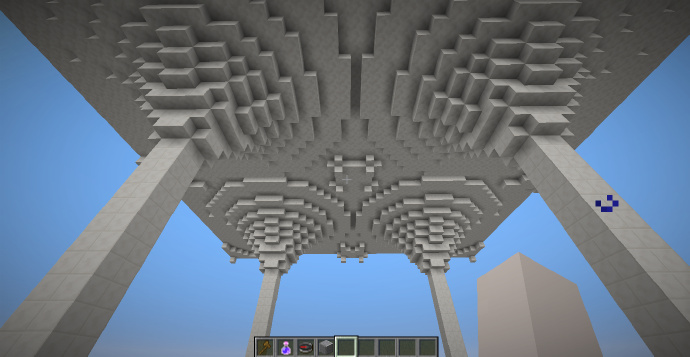
肋形穹顶走廊

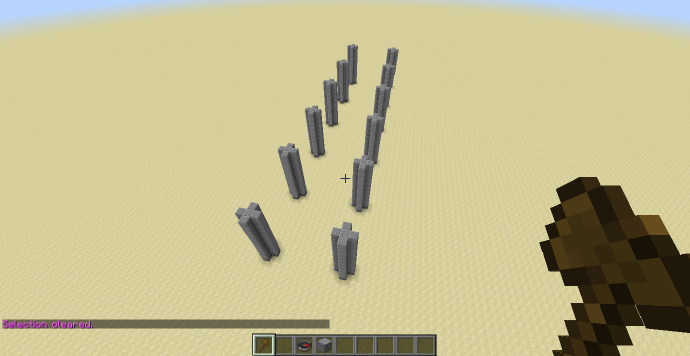
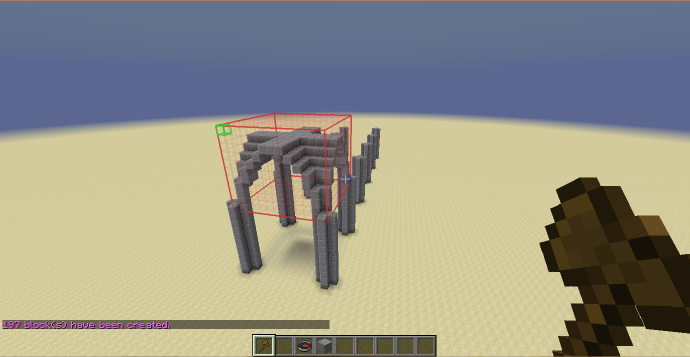
操作目标是在这些柱子上加上肋形穹顶。

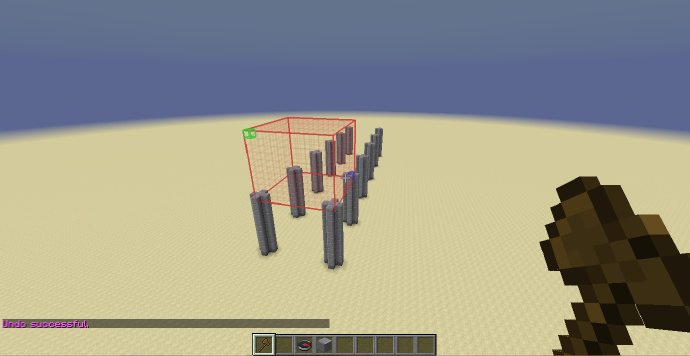
首先确定选区，选区底边的四个点为四根柱子的中心点。

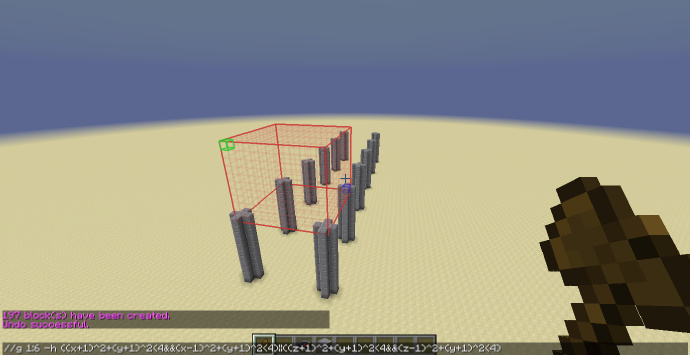
接下来使用肋形穹顶的指令：

//g 1:6 -h ((x+1)^2+(y+1)^2<4&&(x-1)^2+(y+1)^2<4)||((z+1)^2+(y+1)^2<4&&(z-1)^2+(y+1)^2<4)

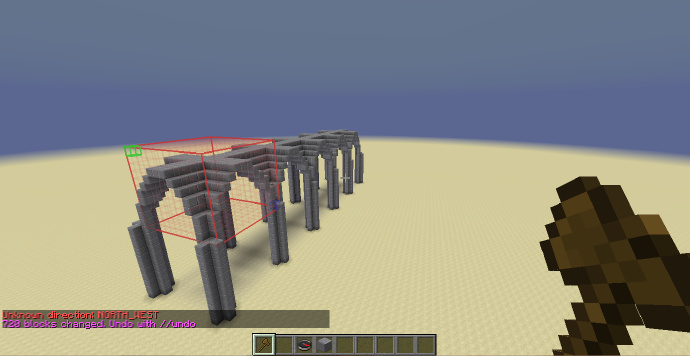
成功生成了穹顶。

接下来使用//stack进行堆积即可，最终效果如下：

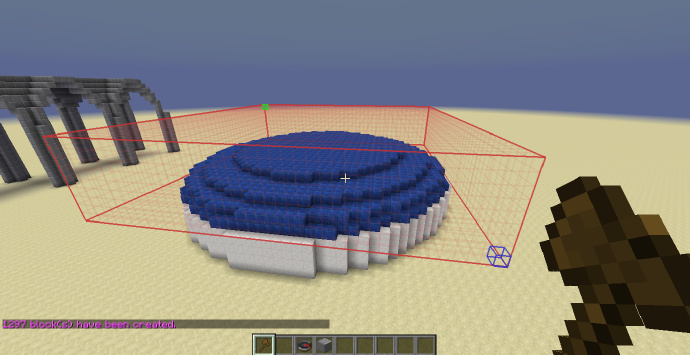
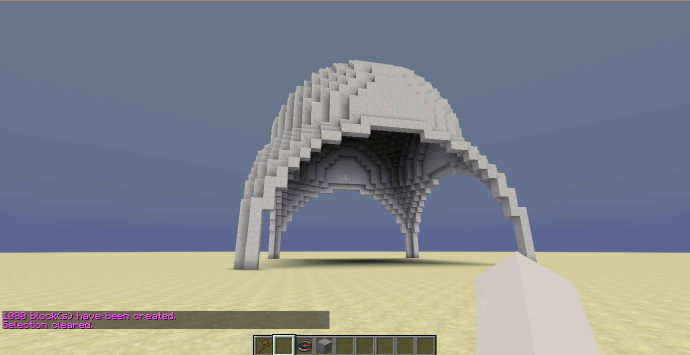
半椭球穹顶

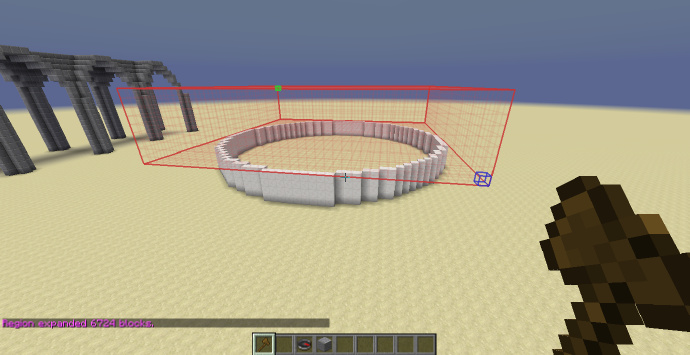
目标为在圆形底座上创建半椭球型的穹顶，首先创建选区。

使用指令：

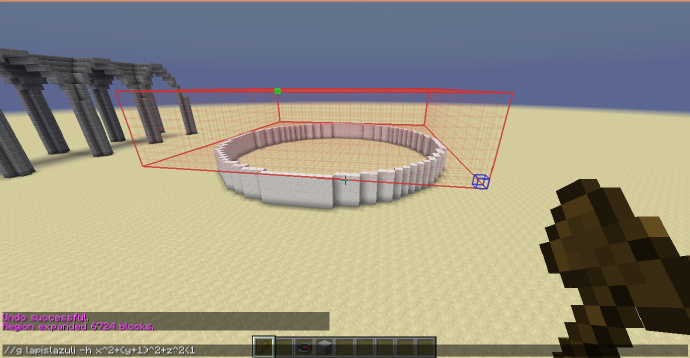
//g lapislazuli -h x^2+(y+1)^2+z^2<1

成功生成，效果如下：

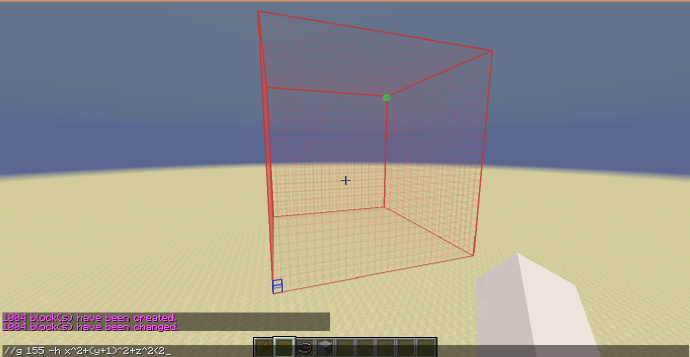
复合式穹顶

使用帆拱与圆形穹顶组合的复合式穹顶首先创建一个帆拱。

//g 155 -h -h x^2+(y+1)^2+z^2<2

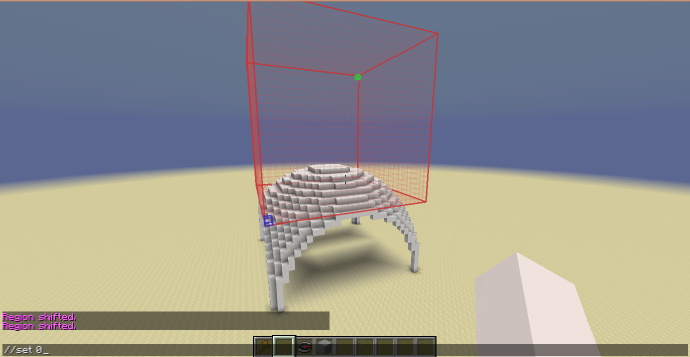
接下来将选区向上平移先前选区的一半高度的距离（这里的选区为30x30x30，所以向上平移15格），移除帆拱的上半部分，留下的下半部分作为复合式穹顶的穹隅。

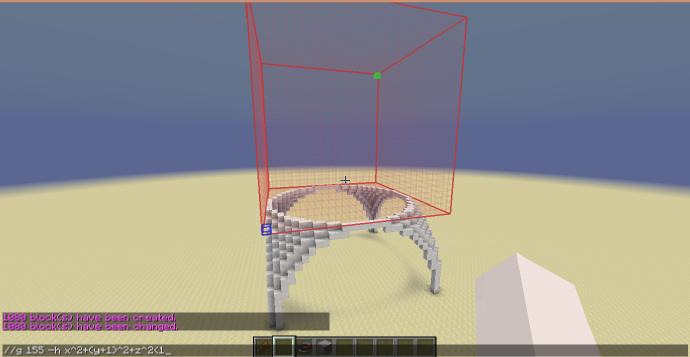
接下来，不改变选区的位置，使用半球穹顶的指令：

//g 155 -h x^2+(y+1)^2+z^2<1

成功生成，效果如下：

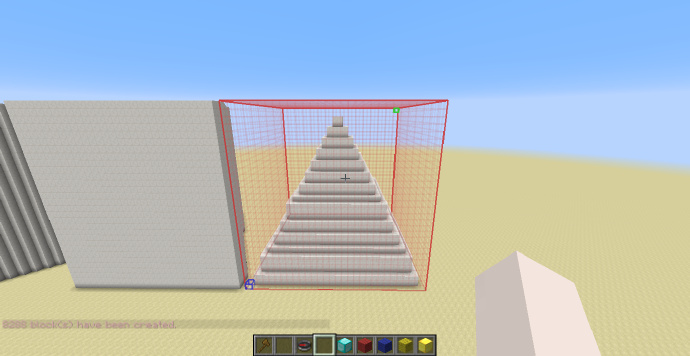
扇形拱顶

前文提到的扇形拱顶，使用圆弧旋转面的组合来完成。

光学三棱柱

一个简单的小作品。

相关资料与来源

• 【WE插件进阶】//GEN命令 建筑屋顶基本型公式总结 by sara_yiwei

例子部分多个例子来源与研究基础(即只提供公式，后续分析由笔者完成)

• 【WorldEdit】WE中//generate指令的研究(教程+讨论向) by Az蓝色轨迹（本文作者）

本文大部分内容研究基础

• Wikipedia数词条

相关专业知识来源

后记

“

我认为这是一个WorldEdit一个非常有潜力，但仍未被发掘的功能，希望更多人能进行更深入的研究，使它的光芒发挥到极致。

”

LocusAzzurro

+关注