抽卡概率计算

^{编 刷 历}

首页 > 攻略 > 抽卡概率计算

---

如果是第一次来，按"Ctrl+D"可以收藏随时查看更新~觉得WIKI好玩的话，请推荐给朋友哦～(◕ω＜)☆
按右上角“WIKI功能→编辑”即可修改页面内容。

抽卡概率计算

2023/11/09

主要结果

马娘池

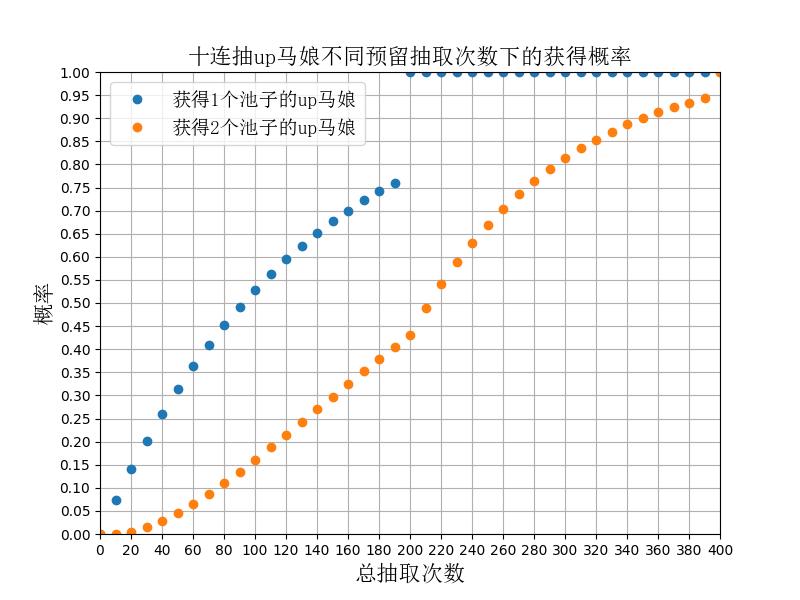
马娘所需的平均抽取次数：

• 单个马娘池up角色：107.3
• 两个马娘池up角色：214.6

支援卡池

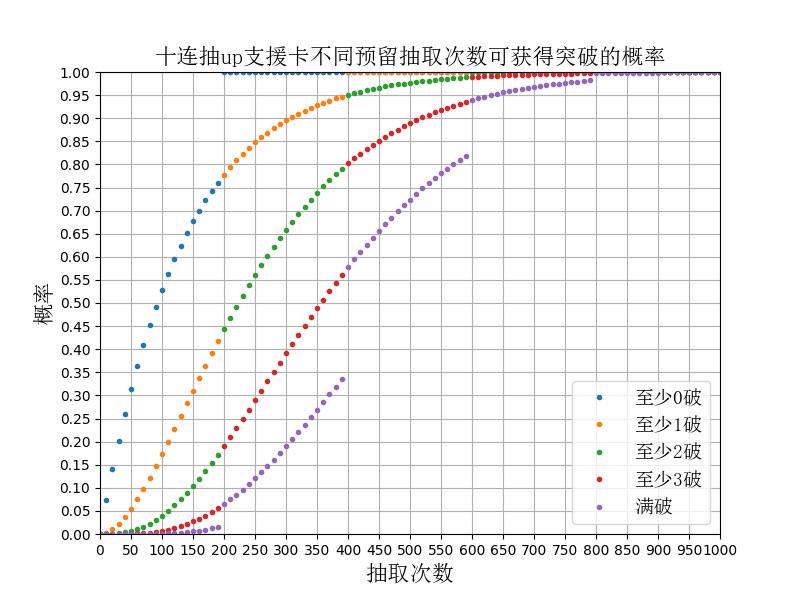
支援卡所需的抽取次数：

• 至少0破：107.3
• 至少1破：188.6
• 至少2破：266.9
• 至少3破：346.7
• 满破：426.8

注意事项

1. 计算中单抽获得目标马娘和支援卡的概率选为0.0075。
2. 抽取马娘和支援卡时只使用十连抽，而非单抽。虽然按单抽和十连抽计算的结果几乎完全相同。
3. 本文的计算考虑了使用抽取次数兑换的马娘和支援卡。
4. 本文没有考虑双up卡池中两个up对象均需要抽取的情况。
5. 本文所给出的结果作为游戏抽卡规划时的参考使用，结果仅具有统计意义。获得的概率高(只要不是1)不代表必定能拿到，平均抽取次数也不代表实际抽卡需要的最高或最低次数。

计算过程

马娘池

P(单抽获得目标马娘) = 0.0075
P(十连抽获得目标马娘) = 1 - (1 - P(单抽获得目标马娘)) ^ 10
P(单个马娘池第n次十连抽才获得目标马娘) =

• 0, n=0
• (1 - P(十连抽获得目标马娘)) ^ (n - 1) * p, 0 < n < 20
• 1 - sum_(n = 1)^19 P(单个马娘池第n次十连抽才获得目标马娘), n = 20
• 0, n >= 21

单个马娘池up角色所需的平均抽取次数 = sum_(n = 1)^20 10 * n * P(单个马娘池第n次十连抽才获得目标马娘)
P(单个马娘池n次十连抽之内获得目标马娘) = sum_(k = 1)^n P(单个马娘池第k次十连抽才获得目标马娘)
P(两个马娘池第n次十连抽才获得目标马娘) = sum_(k = 1)^(n - 1) P(单个马娘池第k次十连抽才获得目标马娘) * P(单个马娘池第n-k次十连抽才获得目标马娘)
两个马娘池up角色所需的平均抽取次数 = sum_(n = 2)^40 10 * n * P(两个马娘池第n次十连抽才获得目标马娘)
P(两个马娘池n次十连抽之内获得目标马娘) = sum_(k = 1)^n P(两个马娘池第k次十连抽才获得目标马娘)

支援卡池

P(单抽获得目标支援卡) = 0.0075
P(十连抽获得n张目标支援卡) = 10! / n!/ (10-n)! * P(单抽获得目标支援卡) ^ n * (1 - P(单抽获得目标支援卡)) ^ (10 - n)
当k < n时，P(n次十连抽获得k张目标支援卡) = 0，当k >= n时：

• P(n次十连抽获得0张目标支援卡) = P(十连抽获得n张目标支援卡) ^ n
• P(n次十连抽获得1张目标支援卡) = n! / 1! / (n - 1)! * P(十连抽获得0张目标支援卡) ^ (n - 1) * P(十连抽获得1张目标支援卡)
• P(n次十连抽获得2张目标支援卡) = n! / 1! / (n - 1)! * P(十连抽获得0张目标支援卡) ^ (n - 1) * P(十连抽获得2张目标支援卡)

+ n! / 2! / (n - 2)! * P(十连抽获得0张目标支援卡) ^ (n - 2) * P(十连抽获得1张目标支援卡) ^ 2

• P(n次十连抽获得3张目标支援卡) = n! / 1! / (n - 1)! * P(十连抽获得0张目标支援卡) ^ (n - 1) * P(十连抽获得3张目标支援卡)

+ n! / 1! / 1! / (n - 2)! * P(十连抽获得0张目标支援卡) ^ (n - 2) * P(十连抽获得1张目标支援卡) * P(十连抽获得2张目标支援卡)

+ n! / 3! / (n - 3)! * P(十连抽获得0张目标支援卡) ^ (n - 3) * P(十连抽获得1张目标支援卡) ^ 3

• P(n次十连抽获得4张目标支援卡) = n! / 1! / (n - 1)! * P(十连抽获得0张目标支援卡) ^ (n - 1) * P(十连抽获得4张目标支援卡)

+ n! / 1! / 1! / (n - 2)! * P(十连抽获得0张目标支援卡) ^ (n - 2) * P(十连抽获得1张目标支援卡) * P(十连抽获得3张目标支援卡)

+ n! / 2! / (n - 2)! * P(十连抽获得0张目标支援卡) ^ (n - 2) * P(十连抽获得2张目标支援卡) ^ 2

+ n! / 2! / 1! / (n - 3)! * P(十连抽获得0张目标支援卡) ^ (n - 3) * P(十连抽获得1张目标支援卡) ^ 2 * P(十连抽获得2张目标支援卡)

+ n! / 4! / (n - 4)! * P(十连抽获得0张目标支援卡) ^ (n - 4) * P(十连抽获得4张目标支援卡) ^ 4

P(n次十连抽至少获得k张目标支援卡) =

• 1, k = 0
• P(n次十连抽至少获得k - 1张目标支援卡) - P(n次十连抽获得k - 1张目标支援卡), k > 0

P(加上兑换结果n次十连抽至少获得k张目标支援卡) =

• P(n次十连抽至少获得k - n // 20张目标支援卡), n < 20 * k
• 1, n >= 20 * k

注：这里a // b表示使用带余数除法时a除以b的商。
至少获得k张目标支援卡所需的平均抽卡次数 = sum_(n = 1)^(20 * k) 10 * n * (P(加上兑换结果n次十连抽至少获得k张目标支援卡) - P(加上兑换结果n - 1次十连抽至少获得k张目标支援卡))