“科学抽卡”理论

^编 ^刷 ^历

如果是第一次来，按"Ctrl+D"可以收藏随时查看更新~觉得WIKI好玩的话，请推荐给朋友哦～(◕ω＜)☆
按右上角“WIKI功能→编辑”即可修改页面内容。

“科学抽卡”理论

前言

本文介绍赛马娘UPSSR抽卡概率计算理论，让各位了解赛马娘抽卡模型。
如果不想看理论讲解，点击目录里的使用示例
若wiki文本可读性差可点击QQ文档其实差不多。
点击计算器页面进入工具。
注意未做手机等移动端适配，建议使用电脑查看，也可以手机浏览器网页并选择“访问电脑版”查看。

N重伯努利试验与二项分布

伯努利试验指的是一次随机试验，它只有两种可能的结果，我们通常称之为“成功”和“失败”。
n重伯努利试验指将同一个伯努利试验独立重复地进行n次。
n重伯努利试验，必须满足以下三个条件：
1.试验次数固定：试验总次数 n 是事先确定的。
2.结果二分：每次试验只有两种可能的结果。
3.独立性与同概率：各次试验相互独立；每次试验中“成功”的概率 p 是相同的。
最经典的例子就是抛硬币。将一枚均匀的硬币抛10次，这里n=10，每次“成功”（比如正面朝上）的概率p=0.5，每次抛掷是独立的。
在n重伯努利试验中，我们最关心的问题是：
“在n次独立重复试验中，恰好发生k次成功的概率是多少？” 这个问题的答案，也就是n重伯努利试验关联的分布：二项分布。
定义X为在n次试验中“成功”出现的次数，X服从参数为n和p的二项分布，其概率质量函数为：

[math]\displaystyle{ P\left(X=k\right)=C_n^k·p^k·{(1-p)}^{n-k} }[/math]

X为在n次试验中“成功”出现的次数；
p是每次成功的概率；n是试验总数；[math]\displaystyle{ P\left(X=k\right) }[/math]表示恰好k次成功的概率；
[math]\displaystyle{ C_n^k }[/math]是二项式系数，公式为[math]\displaystyle{ \frac{n!}{k!·(n-k)!} }[/math]；
而单up抽卡恰好是n重伯努利试验，服从二项分布。

单up抽卡概率模型——有约束条件的二项分布

对于单up卡池或双up卡池只抽其中一个up，服从二项分布。我们想抽对应的up卡，抽取次数为n，抽到up为成功次数k，其p=0.0075。
我们的问题是：
n次试验成功k次及以上的概率。
这个问题是求[math]\displaystyle{ P\left(X\geq k\right) }[/math]的累积概率：

[math]\displaystyle{ P\left(X\geq k\right)=1-P\left(X\lt k\right)=1-\mathrm{\Sigma}_{i=0}^{k-1}P(X=i) }[/math]

看起来很简单！我们将k设为5，对于每个n，就能求出抽到满破及以上的概率，即使不要满破，我们改变k值就可以了，比如我要抽出一破up SSR，让k=2便可；抽出一只up三⭐马娘，让k=1便可。
现在我们考虑单up的保底机制
每200抽有1井，也就是[math]\displaystyle{ int(\frac{n}{200}) }[/math]. 当有1井时，我们抽出4张便相当于抽出5张，即：

[math]\displaystyle{ P\left(X\geq4\right)=P\left(X\geq5\right) }[/math]

由此可见是对k进行减少。
同理在使用彩突时，也相当于我们少抽使用的彩突数量即可，在计算时，1彩突几乎相当于1井*。
(*)使用1彩突至少需要1张，而井则不用，这里不做考虑
对我们的概率公式进行修正：
设T为修正值，其值是投入的彩突数量+井数量。

[math]\displaystyle{ T=h+int\left(\frac{n}{200}\right) }[/math]

将T修正k，

[math]\displaystyle{ P\left(X=k^,\right)=\frac{n!}{(k-T)!·(n-(k-T))!}·p^{(k-T)}·(1-p)^{(n-(k-T))} }[/math]

注意当k<T时，P=1.
在此基础上计算[math]\displaystyle{ P\left(X=k^,\right) }[/math]即可。

单up模型延伸——中途查看概率

在实际抽卡时，往往会选择送抽池。比如送80抽，100抽，120抽。如果我想在抽完送的抽数，中途查看概率，该如何呢？
也很简单，比如我们已经抽了s次，后续的n只需要减去s就可以了，而我们在这之中抽出的up卡，像上式一样并入T即可。

[math]\displaystyle{ P\left(X=k^,\right)=\frac{(n-s)!}{(k-T)!·(n-s-(k-T))!}·p^{(k-T)}·(1-p)^{(n-s-(k-T))} }[/math]

注意抽数小于s的情况我们已经经历过了，当[math]\displaystyle{ n\lt s }[/math]时必然[math]\displaystyle{ P\left(X=k^,\right)=0 }[/math].
(这个延伸同时可以手动比较我们前面送抽抽的是“欧”还是“非”，现在不讨论，将在示例中展示。)

双up抽卡概率模型——由二项分布推广到三项分布

双up相较于单up有一个最大的改动，就是两张都要抽取。这看起来像句废话，但有两个要考虑的点：
1.二项分布失效，要用新的分布计算*。
2.保底机制的修正值要如何分配。
(*):实际上因为三项分布是二项分布的推广，是可以通过条件概率分解成两个二项分布计算。但考虑到要计算条件概率，又要加约束条件实现与单up相同的功能，会比较麻烦。我们直接用三项分布更直观。
解决问题1，我们选择用三项分布。
这里列出二项分布与三项分布的对比：

特征	二项分布	三项分布
试验	n重伯努利试验	n 次独立的三结果试验
随机变量	X(成功次数)	(X1,X2,X3)各结果次数
对应参数	n，p	n，p1，p2，p3
概率公式	[math]\displaystyle{ P\left(X=k\right)=C_n^k·p^k·{(1-p)}^{n-k} }[/math]	以下

三项分布概率质量函数：

[math]\displaystyle{ P\left(X_1=k_1,X_2=k_2,X_3=k_3\right)=\frac{n!}{k_1!·k_2!·k_3!}·p_1^{k_1}·p_2^{k_2}·p_3^{k_3} }[/math]

我们的问题变成：
n次试验X1成功k1次及以上且X2成功k2次及以上的概率。
那么联合累积概率为：

[math]\displaystyle{ P\left(X_1\geq k_1,X_2\geq k_2\right)=\mathrm{\Sigma}_{i=k_1}^{n-k_2}\mathrm{\Sigma}_{j=k_2}^{n-i}\frac{n!}{i!·j!·(n-i-j)!}·p_1^i·p_2^j·p_3^{(n-i-j)} }[/math]

如果我们抽两张满破up，只需要把k1，k2设置为5，对于每个n，就能求出抽到满破及以上的概率。当然改变k值也能求出。

有约束条件的三项分布修正值要如何分配？

在单up情况下，修正值T是都分给一张卡的，这算起来非常简单。双up下要如何分配呢？这里有两位马娘有想法解决，让我们看看哪个正确：
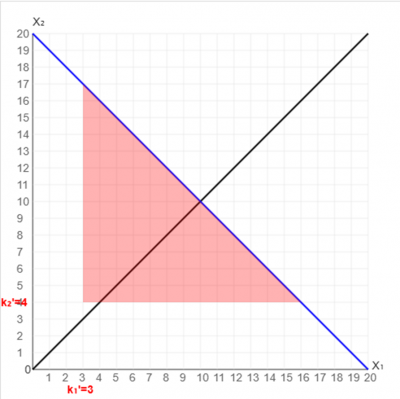
醒目飞鹰同学认为：训练员在最后使用修正(彩突+井)时，这个行为总会是P为最大值时。分配T值使得分配后的[math]\displaystyle{ k_1^,, k_2^, }[/math]有[math]\displaystyle{ |k_1^,\ -k_2^,| }[/math]最小，在其最小时[math]\displaystyle{ P\left(X_1\geq k_1^,,X_2\geq\ k_2^,\right) }[/math]最大。
这是她的证明过程：
在[math]\displaystyle{ p_1=p_2 }[/math]，[math]\displaystyle{ x_1+x_2=C }[/math]为常数*时，画出[math]\displaystyle{ x_2(x_1) }[/math]的图像。
："(*)在输入[math]\displaystyle{ x_1 }[/math],[math]\displaystyle{ x_2 }[/math]时，便会给定。(*)对于每个计算的n也都是定值。"

其中蓝线为约束条件[math]\displaystyle{ x_1+x_2=n }[/math]，这里随便写的20；标注分配后的[math]\displaystyle{ k_1^, }[/math],[math]\displaystyle{ k_2^, }[/math]；红色区域R={[math]\displaystyle{ {(x_1,x_2):(x_1\geq k_1^,,x_2\geq\ k_2^,)} }[/math]}为[math]\displaystyle{ P\left(X_1\geq k_1^,,X_2\geq\ k_2^,\right) }[/math]的区域。问题变成了何时𝑅面积S最大。
区域面积[math]\displaystyle{ 2S=(n-k_1^,)·(n-k_2^,) }[/math]，
因为

[math]\displaystyle{ n\gt k_1^,\gt 0, n\gt k_2^,\gt 0 }[/math]

所以

[math]\displaystyle{ \left(n-k_1^,\right)\gt 0,\left(n-k_2^,\right)\gt 0 }[/math]

又因为
[math]\displaystyle{ (n-k_1^,)+(n-k_2^,)=2n-C }[/math]为定值*
由上两式可知，

[math]\displaystyle{ 2S=\left(n-k_1^,\right)·(n-k_2^,)≤(\frac{(n-k_1^,)+(n-k_2^,)}{2})^2 }[/math]

两倍面积2S在[math]\displaystyle{ (n-k_1^,)=(n-k_2^,) }[/math]时即[math]\displaystyle{ k_1^,=k_2^, }[/math]时最大*，最大值为:

[math]\displaystyle{ (\frac{(n-k_1^,)+(n-k_2^,)}{2})^2 }[/math]

推广至[math]\displaystyle{ x_1,x_2 }[/math]，即[math]\displaystyle{ x_1=x_2 }[/math]时，面积最大，也就是P最大。
上图黑线[math]\displaystyle{ x_1=x_2 }[/math]表示概率点越靠近这条线，概率越大。
由此可见，当[math]\displaystyle{ |k_1^,\ -k_2^,| }[/math]最小时，P最大。
证毕*。
："(*)基本不等式条件不能忘。(*)其实我还有非数形结合的推导，感兴趣你可以试试！"
琵琶晨光同学认为：抽取到最后可能没有满足条件且结果各不同，但只要通过分配T使得最后满足[math]\displaystyle{ X_1\geq k_1^,,X_2\geq\ k_2^, }[/math]即可。这是她给出的关于T的概率公式：

[math]\displaystyle{ P\left(max\left(0,k_1-x_1\right)+max\left(0,k_2-x_2\right)\le T\right) }[/math]

这个计算方法要确定满足条件[math]\displaystyle{ (x_1,x_2) }[/math]的区域：
1. [math]\displaystyle{ x_1\geq k_1,x_2\geq k_2 }[/math]：自动满足；
2. [math]\displaystyle{ x_1\geq k_1,x_2\lt k_2 }[/math]：即[math]\displaystyle{ x_2\geq k_2-T }[/math]；
3. [math]\displaystyle{ x_1\lt k_1,x_2\geq k_2 }[/math]：即[math]\displaystyle{ x_1\geq k_1-T }[/math]；
4. [math]\displaystyle{ x_1\lt k_1,x_2\lt k_2 }[/math]：即[math]\displaystyle{ x_1+x_2\geq k_1+k_2-T }[/math]。
再对于满足区域求和即可。
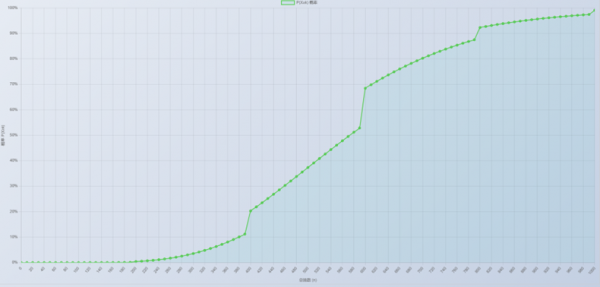
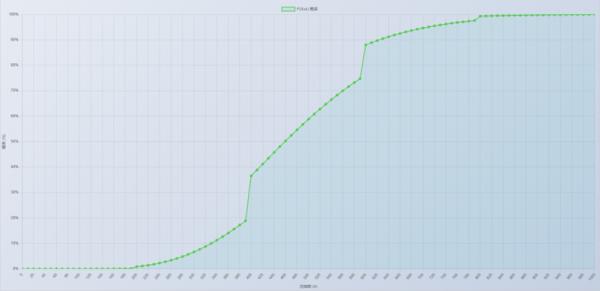
让我们看看上面两位实际求得的情况，我们都是抽两张up SSR满破，只用一个彩突：
这是醒目飞鹰算的：

这是琵琶晨光算的：

虽然图比较小看不太清具体数值，但是明显图1概率偏小，图2概率偏大。
上帝视角答案是琵琶晨光是对的，醒目飞鹰算错了。
："你算的概率低太多了！" "又要挂科了！"：
琵琶晨光你来解释一下吧。
:[[math]\displaystyle{ P\left(max\left(0,k_1-x_1\right)+max\left(0,k_2-x_2\right)\le T\right) }[/math]这个概率等价于
P(∃[math]\displaystyle{ T_1,T_2 }[/math]满足[math]\displaystyle{ T_1+T_2=T }[/math],使得[math]\displaystyle{ X_1+T_1≥k_1,X_2+T_2≥k_2 }[/math])
表示分配[math]\displaystyle{ T_1,T_2 }[/math]，能够同时使[math]\displaystyle{ X_1 }[/math]和[math]\displaystyle{ X_2 }[/math]达到或超过阈值[math]\displaystyle{ k_1 }[/math]和[math]\displaystyle{ k_2 }[/math]的可能性。
只要[math]\displaystyle{ max\left(0,k_1-x_1\right)+max\left(0,k_2-x_2\right)\le T }[/math]，就存在一种满足条件的分配方式，并不关心分配后如何。
而醒目飞鹰考虑的没问题，训练员在最后使用修正确实是P最大时。
但她是先分配后计算，而实际情况时先抽卡最后分配。
换种说法是在我的基础上最小化[math]\displaystyle{ |k_1^,\ -k_2^,| }[/math]，这种分配方法只是众多分配中P最大的，并没有考虑其他分配方法。
如果把她考虑的情况写出来就是：
P(在[math]\displaystyle{ T_1,T_2 }[/math]满足[math]\displaystyle{ T_1+T_2=T，|k_1^,\ -k_2^,| }[/math]最小,使得[math]\displaystyle{ X_1+T_1≥k_1,X_2+T_2≥k_2 }[/math])
可见分配时更严格，增加了新的约束，因此更难满足。 ]
现在保底机制分配解决了，最后再加入中途确认概率，跟单up一样只需要对应值减去已有即可。
总的来说，单up是有约束条件的二项分布，双up是有约束条件的三项分布。

使用示例

下面大致介绍一下怎么用。

注意只有通常的单双SSR卡池才适用，涉及要抽取二⭐与SR的 UP卡池、付费萝卜step卡池不适用。
最上方选择模式；
预期张数：填入想要抽的张数，要抽一只马娘时填1；
注意这是总的张数，如果你要抽5张，在中途抽出2张，也不要从5改成3。
已投入抽数：中途使用时填入已经抽了多少抽；
投入虹结晶数：只需要填入最后你要使用的，不需要自己算井；
已有张数：在中途使用填入已有的，不需要自己算井；
“因子研究”图标是计算，在双up点击后会卡顿一会儿，正常现象。
以下是个人观点！！
我们还可以手动观察送抽是“欧”还是“非”：
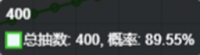
比如我们用送抽的100抽抽爱如往昔，先按上图设置查看初始概率
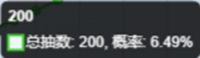
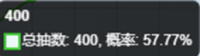
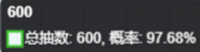
我们再在已投入抽数填入100，假设我们100抽出1张
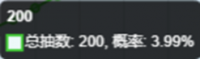
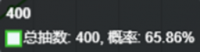
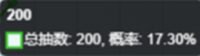
假设我们100抽出2张：

初始
1
2

对比看出因为前100抽已经抽过了，所有200抽的概率下降了，但是400和600抽更高了，笔者认为如果要2井满破那送抽出1张算正常水平或很好了。
如果出两张那赚飞~~~了！！！！后面“正常发挥”就能2井满破。
其他情况自己试试吧！
：“最好抽完免费送的再抽，理性抽卡！”

醒目飞鹰的Q&A部分

：“为什么用概率显示，不用期望呢，或者不显示平均xx抽x破？”
“对概率不敏感的训练员，如果直接写出获得k至少需要多少n的话，他们会认为达到是理所应当，没有就会很沮丧，这样影响很不好。~~不如像数码一样来快乐抽卡。~~”：
：“~~恶狼不讲仁慈！抽一只up三星马娘需要108抽！~~”
：“真让人头大！”