- 点击右上角🔍，可以搜索 WIKI
狮子座
阅读
2021-02-28更新
最新编辑:封面图收藏家
阅读：
更新日期：2021-02-28
最新编辑：封面图收藏家
狮子座是bilibili代理的手机游戏《方舟指令》中的登场角色。方舟指令狮子座图鉴数据，由WIKI成员提供，转载请标明来源链接！
 星辰 轩辕焰影 狮子座
| ||||
|---|---|---|---|---|
|
编号 | NO.111 | 稀有度 | SR |
属性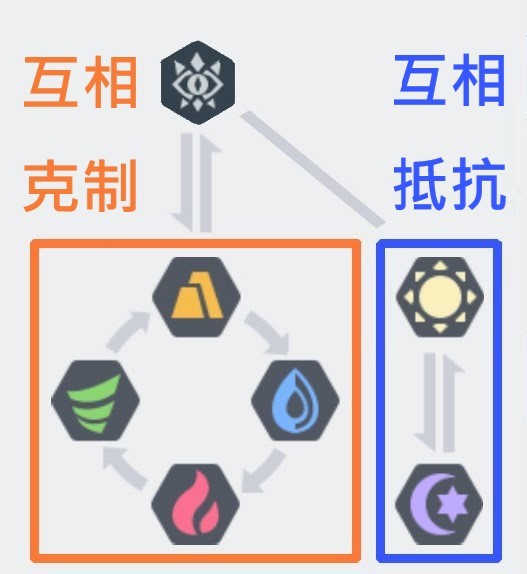
|
 火
|
消耗 | 9 | |
| 出没地点 | ||||
| 活动掉落点 | ||||
| 誓约破除 | 10  、5 
| |||
| 实装日期 | 2019年08月23日
| |||
| 性能 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 100 级 无圣器无核心无能源分配能力值 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 「天赋」 狮王之裘 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 攻击造成一次伤害后可积累一层“狮王之裘”效果，被技能攻击时可以减伤20%、提升自身1级魔攻且消耗一层“狮王之裘” | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
生命
速度
物攻
物防
魔攻
魔防
| 进化 | ||||
|---|---|---|---|---|
| 二星 ☞ 三星(Lv.15) | |
| ||
| 2000 | 4 | |||
| 三星 ☞ 四星(Lv.35) | |
 |
| |
| 3000 | 12 | 16 | ||
| 四星 ☞ 五星(Lv.55) | |
 |
| |
| 4000 | 16 | 32 | ||
- 技能
- 怒气技能
| 技能 | |
火、类型:魔法
光、类型:辅助
| 立绘 |
|
| 画师 |
| 鳩山井鶴+ |
| 声优 |
| 水间友美+ |
| 台词 |
|---|
|
| 协会内台词 |
|---|
|
|
| 受到火系技能伤害减少5％ |
| 圣器 | ||
| 推荐 | 推荐人 | 推荐理由 |
|---|---|---|
神明考究
黄道星座之一，传说中刀枪不入的巨狮。
【神话传说】
赫拉克勒斯是宙斯与凡人的私生子，他天生具有无比的神力，天后赫拉也因此妒火中烧。在赫拉克勒斯还是婴儿的时候，就放了两条巨蛇在摇篮里，希望咬死赫拉克勒斯，没想到赫拉克勒斯笑嘻嘻的握死了它们，从小赫拉克勒斯就被奉为“人类最伟大的英雄”。
赫拉当然不会因为一次失败就放弃杀死赫拉克勒斯，她故意让赫拉克勒斯发疯后打自己的妻子，赫拉克勒斯醒了以后十分懊悔伤心，决定要以苦行来洗清自己的罪孽，他来到麦锡尼请求国王派给他任务，谁知道国王受赫拉的指使，果然赐给他十二项难如登天的任务，必须在十二天内完成，其中之一是要杀死一头食人狮。
这头狮子平时住在森林里，赫拉克勒斯进入森林中找寻他，只是森林中一片寂静，所有的动物，小鸟、鹿、松鼠都被狮子吃得干干净净，赫拉克勒斯找累了就打起嗑睡来。就在此刻，食人狮从一个有双重洞口的山洞中昂首而出，赫拉克勒斯睁眼一看，天啊！食人狮有一般狮子的五倍大，身上沾满了动物的鲜血，更增添了几分恐怖。克勒斯先用神箭射他，再用木棒打他，都没有用，食人狮刀枪不入，最后赫拉克勒斯和狮子肉搏，过程十分惨烈，但最后还是用蛮力勒死了狮子。
食人狮虽然死了，但赫拉将食人狮丢到空中，变成了狮子座。
誓灵导航
- 水
- 火
- 风
- 土
- 光
- 暗
- 虚无
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- 阿斯加德
- 幻想
- 阿瓦隆
- 高天原
- 奥林匹斯
- 九霄
- 赫里奥波里斯
- 混沌
- 婆罗多
- 大韩
- 签到
- 联动
| 星辰 | ||||||||||||
| 时历 |
| Bilibili | ||||||
| 摸鱼组 | ||||||
| Vsinger | ||||||
| 星之梦 | ||||||
| 约会大作战 | ||||||
| 游戏人生 | ||||||
| CLANNAD | ||||||
| 少女终末旅行 | ||||||
| 神楽Mea | ||||||
| 点兔 | ||||||
| 料理次元 |
沪公网安备 31011002002714 号