科研策略专题攻略
阅读
2024-07-10更新
最新编辑:坐看云起i
阅读:
更新日期:2024-07-10
最新编辑:坐看云起i
策略规划参考
一图流
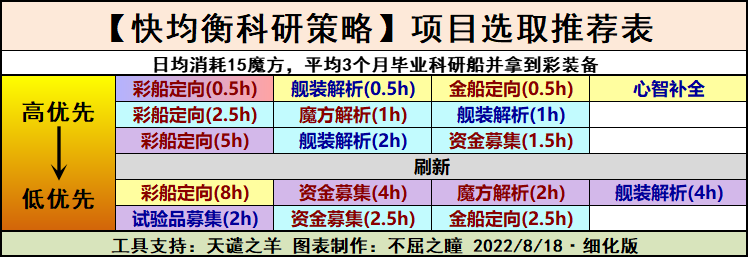
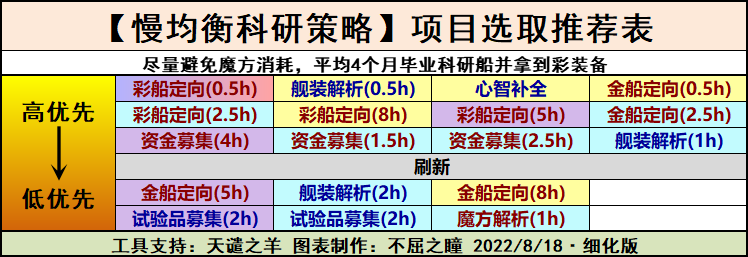
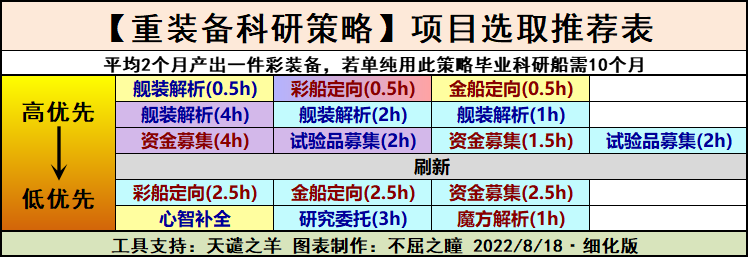
简单给出三类参考策略,力图涵盖多数需求。主要应用于五到八期科研(一至四期追赶机制较完备且收益一般,一般不建议军部研究室选一至四期)。
如需对科研策略进行详细定制,请阅读第二章后,下载使用科研计算工具。
项目分析讲解
对各类科研项目进行定性评述。项目简称:编号字母+项目时长,例如D2.5即2.5小时定向研发。
魔方解析(H)

|
|
金船定向(D)

|
|
- 策略变通简介
- 蓝图型:彩船D / H1; 装备型:Q; 综合型:G / 金船D2.5
- 组合效应:【蓝图型 + 装备型】的产出强于【综合型 + 综合型】
- 短时优势:当兼顾两类产出时,出于均衡考虑,时间偏长、产出单一的项目优先级降低。
- 顺位改变:视情况灵活调整优先级。举例,装备型 > 蓝图型 > 综合型 → “装备为主,彩船加速”。
- 特定削除:若节省魔方少做H1,此时蓝图型项目缺失,用综合型补充。装备产出同时被综合型强化,因此装备型优先度降低(慢均衡的产生)。
宏观思想
- 目前,科研队列的实装极大提升了科研系统的便利性,早中晚各上线一次即可基本完成持续运转。如前面策略图所言,3~4个月即可彩船彩装备双收,而科研系统每一期的实装间隔约为1年,因此补全往期科研也有了充分的余地。对强度有追求的玩家务必有效利用这一系统。
- 科研船的完成必然需求物资/魔方,慢均衡策略实质是用更高的物资投入抹平了魔方投入。因此,对于初接触科研系统的新玩家来说有资源压力,甚至舰装解析也可能遇到装备部件不足的问题。这里给出的建议是,根据自己的资源情况,前期有计划地放弃一些高产出科研项目,用没有实质投入的EBCT类代替(其中E、B类的产出相对好),或者用科研规划器定制一个低投入科研策略。优先进行主力队伍培养,早日推到高级图刷取大量物资,之后再回头加速科研也不迟。通常用慢均衡策略追赶即可。
- 一个合理的科研策略,关键在于高收益项目与低收益项目的整体顺位无误,而不在于仔细推敲每一个项目的优先级。调转两个地位相近项目的顺位,一般只带来微弱影响,或者有利有弊,这就是科研策略的模糊性。在策略图中虽然使用定量价值衡量方法排序了每一个科研项目,但同一行内地位也是基本相近的。因此,想要把握构建科研策略的方法,并非必须系统学习现有的复杂理论,总的来说:
- (1)参考项目分析讲解,有一个定性的认知;
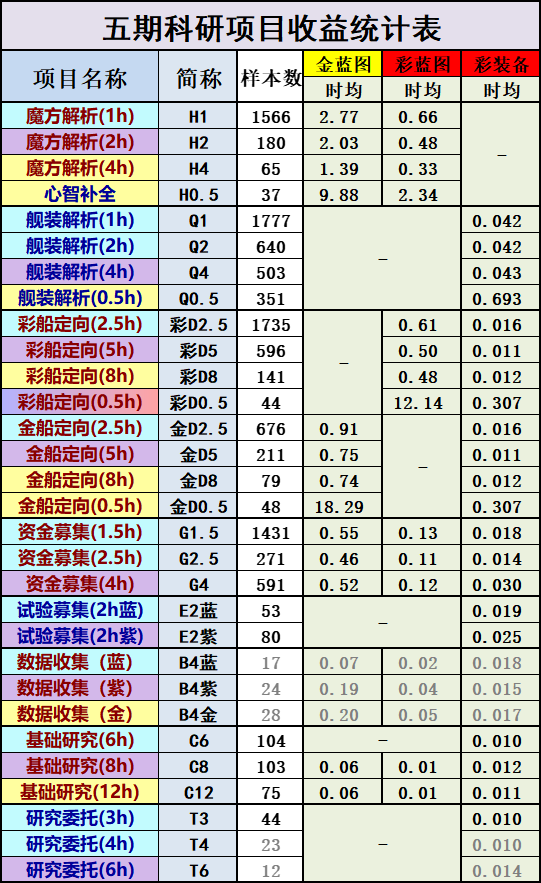
- (2)查阅科研项目统计中的项目收益图,加深定量认知;
- (3)价值衡量理论的核心就一句话——高收益项目时间越长越赚,低收益项目时间越长越亏;
- (4)实践层,根据自身需求适时调整。
策略计算工具
基于加权性价比算法的科研规划表格
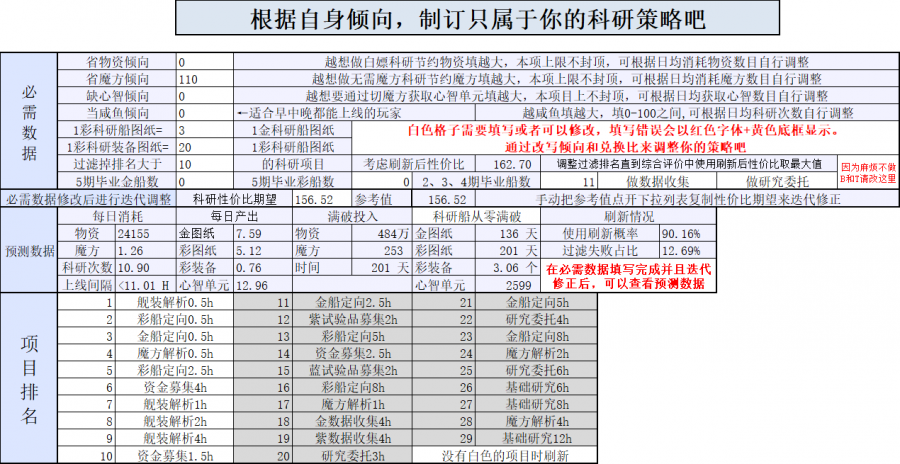
- 结合自身实际情况,填写表格参数。初次使用时建议参考本节末尾的使用过程举例。
- 根据当前科研状况进行调整。
- 此处点击下拉列表给出的数值进行迭代!反复数次直到与右侧参考值相等为止。
- 细化过滤排名,获取最大性价比。
- 查看投入产出是否符合自身需求。
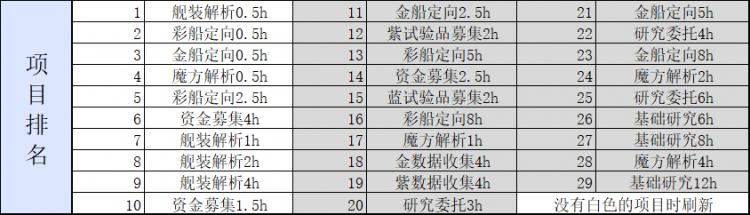
- 查看科研策略。表格下方还有更多精细数据。
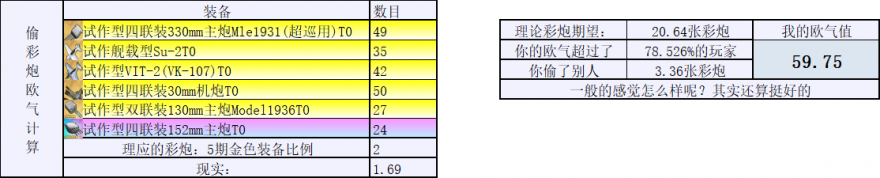
- 小工具:切换“欧气计算表”,填写当前图纸数量,看看自己的产出是否达到了策略的预期?
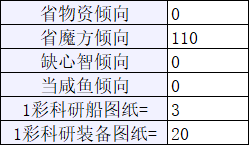
一开始,不知道具体的性价比、倾向、过滤模式怎么填,所以都是随意填的数字,如下图

接下来,看见给出了新的性价比参考值,这时就需要手动点击下拉列表来同步数值
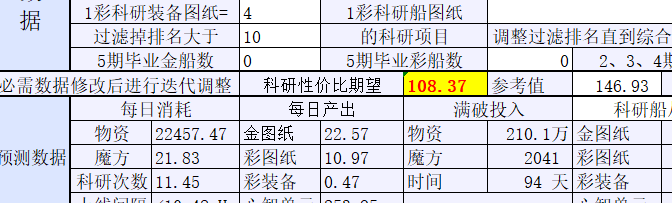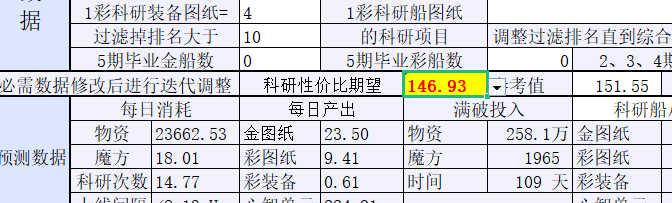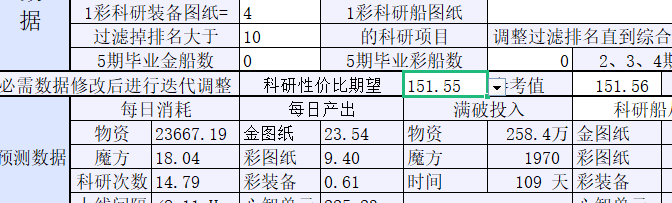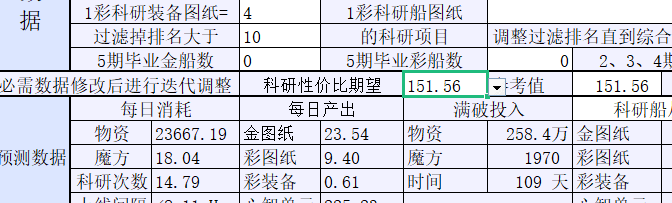
多次迭代后数值不再变化了,这时就可以查看支出和收益的期望,以及科研项目排序了。
可以看见每天切的魔方实在太多了,这时就应该调高省魔方倾向的数值。
金船毕业远比彩船快,这时应该调高金彩兑换比
但是调多少呢?我也不太清楚,总之随便改一下吧。这样修改后再走一遍手动迭代再看看吧
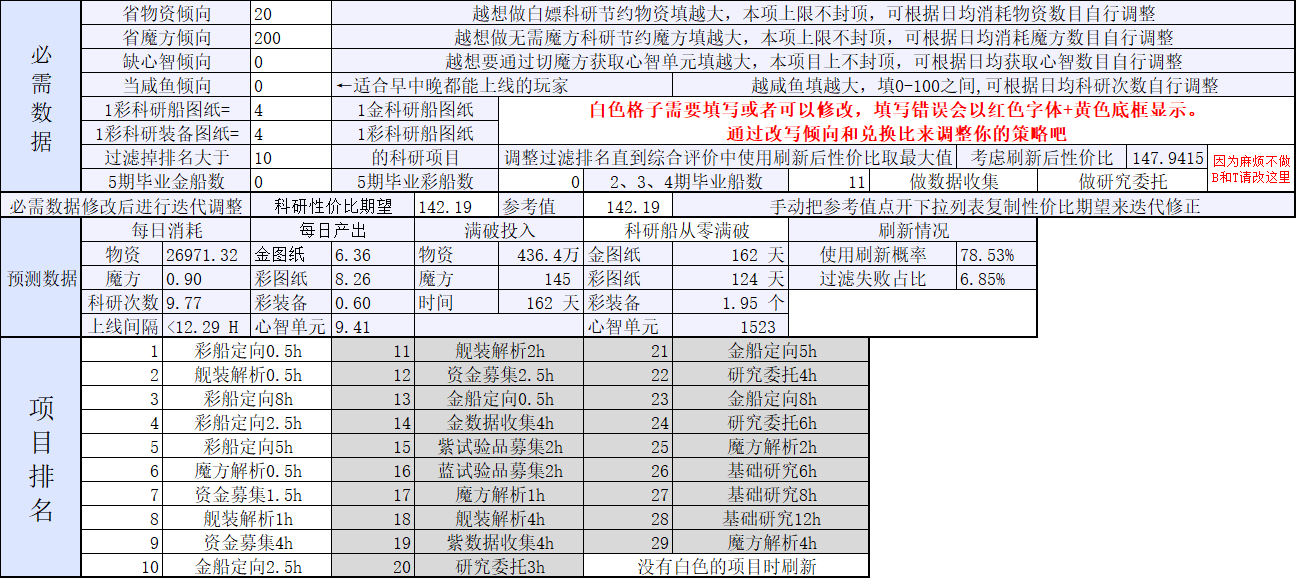
现在给出的倾向就合理多了,而且收益、毕业速度之类的都很不错。
但是看起来金船定向的排名实在太低了,导致金船毕业甚至比彩船慢。这似乎是因为彩与金图纸兑换比设置得太高的缘故。所以还是得继续修改
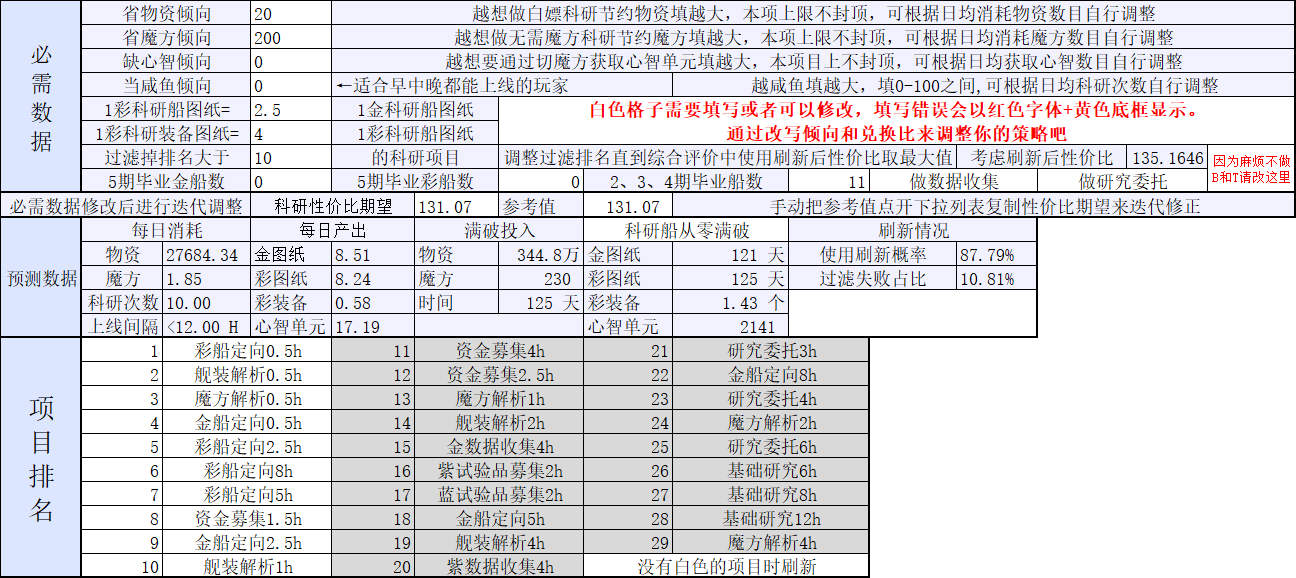
现在的数据就相当不错了,收菜次数、魔方消耗、物资消耗等都在预期之内,收入也符合我个人的预期,可以保留下来作为我科研项目选取的指导。
保存方法:选取你想要保存的表格部分,按ctrl+c复制,可以直接粘贴到QQ聊天框
当然,你使用QQ的截图功能、excel自带的复制为图片功能等也是可以的。
自定义限制条件的科研规划器
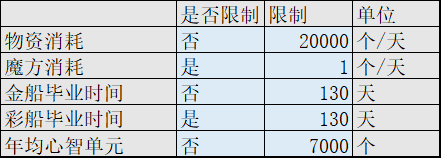
- 打开“策略限制表”,根据自身需求,填写限制条件。
- 限制条件中无装备选项,因为规划器会自动得出给定条件下装备收益最大化的方案。
- 根据当前科研状况进行调整。
- 确认限制表和输出表均已关闭后,打开“keyan”,等待程序运行完成。若长时间无法运行完成,可能需要考虑放宽限制条件。
- 打开“策略输出表”,得到三阶段科研策略。
策略理论研究
概述
科研策略,一般指在军部研究室中选取各种科研项目的优先级。我们往往认为各项目的选取优先级在一定的时间内保持不变,可将之称为“静态策略”。对于科研策略的研究,可以分为正问题与反问题:
(1) 给出一个科研策略,如何预测其投入产出?
(2) 给出投入产出限制,如何计算符合需求的科研策略?
本文的全部研究内容,均为围绕这两个问题,对静态策略展开的研究。而在选取项目历程中随时可能调整优先级即“动态策略”则超出了本文的范畴。(例如,根据自身彩装备进度不断调整舰装解析的优先级,是一种典型的动态策略。尽管对于动态策略的建模分析有较大的难度,但实践中在对静态策略有深入理解的基础上不难对项目选取优先级做出动态调整。另外,科研规划器给出的分段静态策略也可以认为是向动态策略的逼近。)
科研项目统计
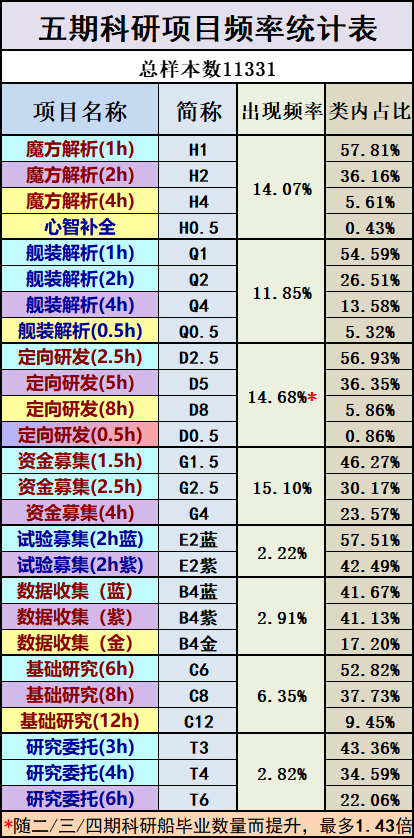
军部研究室的内容实质上可分为两类随机事件:(1) 随机刷出5个科研项目;(2)完成科研项目时随机产出。因此,为了对科研策略进行较为准确的评估,首先要进行的工作是对这两类随机事件进行统计。进一步讲,我们关注的是项目的刷出概率与产出期望,这是构建科研策略理论的基石。
- 部分细节内容此处不展开,可参看:科研五期项目收益与频率统计
项目刷新模型——投入产出计算
目前对项目刷新与选取的分析往往基于独立刷新模型,即假设5个科研项目栏位的刷新相互独立。结合科研倾向机制,有3个栏位固定刷新五期科研,而具体项目的刷出概率由统计数据确定。在此基础上,可计算得到“选取某一项目的概率”为:P( 刷出该项目 ∩ 未刷出更高优先级项目 )。
得出各项目的选取概率后,结合项目收益统计数据即可得到给定策略的投入产出预测值,推导如下:

投入产出的计算方法完全一样。项目刷新模型建立了从策略到产出的联系,是构建科研策略理论的支柱。
- 科研项目每日还有一次手动刷新机会,因此选取优先级中刷新也占有某个顺位。加入刷新后策略的投入产出可利用日均科研选取次数近似计算,此处不展开叙述。另外,刷新实际上涉及到动态策略问题,即一天中越晚的时刻越倾向于用刷新(否则若一天之内刷新次数未用可视为浪费),这点可以在科研规划表格中切换“当前时间过滤排名”查看。
- 独立刷新模型没有完全还原科研刷新机制,事实上多数项目都有同名不同时刷新的规则。刷新模型研究初期曾提出过所谓采样模型,即利用大量实际刷新样本来模拟真实科研情况,发现得到的结论与独立刷新模型基本一致,因此认为独立刷新模型是一个很好的近似。加之其具有理论分析更方便的优点,故最终作为标准模型被保留下来了。
加权性价比算法——项目价值衡量基础
项目刷新模型完成了科研策略研究中的正问题求解。我们进一步思考:能否构建一个对科研项目的定量化评价标准,从而根据自身需求对科研项目进行排名,完成反问题求解?这一问题的提出由来已久,它伴随着科研策略理论的整个研究历程。
在尚未有系统理论的初期,我们往往以项目的时均产出作为其评价标准。但不难发现这一标准存在不足之处:(1)Q1、Q2、Q4的时均装备产出相同,如何衡量其价值?直觉告诉我们,在装备策略中,应该优先选取时均较长的Q4,这样可以减少我们刷新不到Q系项目的概率,而时均产出无法对这一选取倾向做出解释。(2)再次考虑装备策略中的情况,H1全无装备产出,C12有极低装备产出,哪个价值较大?直觉告诉我们,选取Q1浪费一小时进行刷新,比C12浪费12小时的价值要大,而时均产出却只能认定C12更高,无法进一步做出解释。
因此,我们仔细考虑选取一个项目从长远角度看产生的影响。设有一很长的时间周期T;设一策略整体的时均产出为A;设一科研项目时长为t,时均产出为a。选取该项目后,时间周期T上的总产出B为:B = at + A(T - t) = (a - A)t + AT。注意时间T很大,因此T - t时间段的时均产出认为是A。由于时间T是事先给定好的数值,策略的时均产出A对于不同项目也都一致,因此AT一项可以删去,则选取该项目产生的实际价值为(a - A)t。对于这一表达式的具体解释为:一个科研项目的价值,是其时均产出与策略整体时均产出相减后,再乘以项目时长。当科研项目的时均产出高于策略的时均产出,项目时间越长越赚;当科研项目的时均产出低于策略的时均产出,项目时间越长越亏。
有了这一思想,就可以弥补单纯时均产出观点的不足之处:尽管三种Q系的时均一样,但考虑到Q系为装备产出优势项目,时均产出显然高于策略时均,因此Q4时间长价值大;H1和C12都是在亏,但C12的时间过长导致价值反而不及H1,即劣势项目注重刷新收益。
由于我们已经完成了正问题求解,因此可由项目选取优先级得到策略的时均产出A。但优先级即价值的排序,本身就需要用A才能得到,如何解决?为此,提出迭代优化方法:
(1) 将项目按时均产出排序,计算整体时均产出A。
(2) 以现有A值为依据,对科研项目进行价值计算,并重新排序。
(3) 计算现有排序的整体时均产出A,若有变化,重复步骤(2)(3),若无变化,迭代终止。
实践表明,每次迭代均会提高A值,且简单迭代数次后就会收敛。
对于单一产出目标,我们很容易用迭代优化方法计算出时均产出最大化的策略。再深层考虑:(1)蓝图、装备乃至心智均为产出目标时,如何衡量项目的产出?(2)如何将资源限制如魔方、物资引入到优先级排名中?这最终引出了加权性价比算法:一个科研项目的投入,可以视为时间、魔方、物资消耗的加权求和;一个科研项目的产出,可以视为蓝图、装备、心智产出的加权求和。产出除以投入,可以得到该项目的性价比;各项目的产出与投入,分别用其选取概率加权求和,相除可以得到科研策略整体的性价比。一个科研项目的价值,应推广为其性价比与策略整体性价比相减后,再乘以项目投入。整体性价比的计算,依然可以用迭代优化方法得到。
计算科研项目投入产出的权重,是人为给定的,这就是科研规划表格中填写各倾向数值后迭代数次就可以给出科研策略推荐的原理。加权性价比算法在实践中发挥出色,藉此构建出了科研策略理论的殿堂。
模拟退火算法——带约束优化问题的求解
虽然运用加权性价比算法可根据自身需求调整科研策略,但其中用到的权重参数并非需求的直接表现。我们往往会提出诸如“毕业时间有多快”、“资源消耗有多少”等需求,此时需要对权重参数进行反复调整,尝试得到合乎需求的策略。因此,该方法在使用上仍具有一定复杂性。
那么,我们能否利用计算机来完成权重参数调整,从而简化操作,加大优化力度?为此,先介绍模拟退火算法:
(0) 一般优化问题中,具有向量形式的输入X与输出E。设定标量评价函数C(E),优化目标为找到一个输入使得评价函数达到最小值。设定“温度”参数T。
(1) 初始化输入X,并计算评价函数C(E)。
(2) 对当前输入X进行一次随机扰动,得到新输入X',并计算对应输出E',得到评价函数的增量ΔC = C(E') - C(E)。
(3) 若ΔC < 0,接受X'作为新的X;若ΔC > 0,以exp(-ΔC/T)的概率接受X'作为新的X。然后降低温度T,重复步骤(2)(3),直到满足终止条件为止。
模拟退火算法的过程是计算机不断尝试改变输入X,一旦找到了减小评价函数的途径就接受,即使增大了评价函数也会考虑“绕一个弯子”再减小评价函数的可能性。而温度T的存在使得算法在优化后期愈发倾向于保留已优化好的X。通常在介绍模拟退火算法时以求解最小值为例,当然求解最大值的原理也是一样的。
将模拟退火算法应用到科研策略的优化上去,就得到科研策略的模拟退火算法:
· 输入X为加权性价比算法中的各权重参数,输出E为迭代完成后策略的投入产出。
· 评价函数C(此处称为适应度)的计算方式:装备产出越高,适应度越高;资源投入与毕业时间超出限制越多,适应度越低。
此处使用“给定资源投入与毕业时间限制,最大化装备产出”的逻辑。算法为了合理处理问题涉及到的一些细节不展开叙述。
模拟退火算法借助计算机实现了加权性价比算法中权重参数的调整过程,从而大大提升了使用的便捷性,并能完成手工难以实现的细致优化。这一方法的提出代表了科研策略反问题的有效解决,拂去了理论殿堂上的乌云。
岁月史书
- 2019年7月
- 井号5467等前辈们对于科研二期项目收益的统计结果发布,正式揭开了科研策略定量化分析的篇章。科研三~五期每年均有一轮统计工作。
- 2021年9月
- 不屈之瞳提出以采样模型模拟实际科研,提出迭代优化方法对科研项目进行价值衡量。十五号线发车前提出独立刷新模型作为项目刷新机制的替代。
- 2021年11月
- 天谴之羊提出加权性价比算法,成为当前科研策略理论的基础。
- 2022年7月
- 天谴之羊提出以遗传算法或模拟退火算法生成科研策略(后来只保留模拟退火算法),最终完成了给定限制条件下科研策略的三段规划。
- 科研策略理论的发展离不开每一代成果的积累,当前虽已进入高度实用化的阶段,仍具有进一步探索的可能性。
不要停下来啊 - 致敬每一位付出过一点一滴努力的人。















 沪公网安备 31011002002714 号
沪公网安备 31011002002714 号