技能覆盖率计算公式
阅读
2023-03-16更新
最新编辑:負けん気な瞳
阅读:
更新日期:2023-03-16
最新编辑:負けん気な瞳
目前存在的问题:没有补充结尾处的名单,请大家以数学推导、证明过程为主,核心是给出的公式。
常陆茉子审核意见:暂只计算了主炮触发覆盖主炮的情况,并不能代表主炮开炮....使得鱼雷/防空炮如何如何等的情况,此时使用主炮代替会有一些误差。
本条只能适用于:开炮时,对本武器附加某种加成,不涉及其他武器;或开炮时,获得某种buff,且对这种buff只需要计算平均覆盖率。
填写主炮CD时,请注意卡炮、前后摇、开火时间等的影响。
使用情况与预设参数
使公式绝对准确的必要条件:触发条件为“开炮/防空炮时”,且开炮间隔固定。
(目前由于卡炮等问题,开火间隔并不固定,这对以下a、b的取值会有很大影响(要取整),因此只能用于计算开火间隔固定的情况。否则就要请出计算机,模拟前排移动和卡炮了。)
其实不止是技能,例如点燃、命中敌人时,甚至受击等等,也可以等效视为某种的开炮时的技能。
只要他满足了触发时机(在内置cd外时)的间隔固定这一最重要的条件即可
其实略微不固定也可,主要是不能使得下述a、b的值取整后变动,从而影响公式
因此需要主炮尽量不卡炮、防空圈内一直有飞机等
若变动较大,则本公式准确性会下降,
但也可以将实战中可能出现的不同的值分别代入,大致估计实际情况波动范围
另外也不太适用于多底座开火的情况,因为不同底座时间间隔较短
但由于正常情况下不同底座开炮时间间隔极短,在计算随时间的覆盖率时,可近似视为两炮同时发射,从而满足使用条件,例如休斯敦(不过目前主要用于单底座驱逐等,此时没有误差)
而其他情况若实在不满足开炮间隔固定,则情况会变得极多,但若cd覆盖的轮数均较短,也可以通过枚举计算之,如布莱默顿,见专栏[1](最后三种情况计算有小错误)
设技能描述为:开炮时,有c概率,使得接下来t2秒内,获得某效果,内置cd为t1,每两轮炮开火间隔(即每轮cd)为T
则设(以下均向下取整,注意每轮cd需加上前后摇)
内置cd/每轮cd+1=[t1/T]+1=a轮,即内置cd覆盖的开炮次数(触发技能的那一炮也算)
持续时间/每轮cd+1=[t2/T]+1=b轮,即技能触发覆盖的开炮次数(触发技能的那一炮也算)
abc即为所需要的所有参数
增伤技能
具体的来说,若此技能只与触发技能对应的炮有关(大部分情况就是主炮增伤)
也就是你只关心开火时这个时间点是否在覆盖之下,则适用此情况
设k为无穷轮覆盖率,即无穷轮后每次开炮时有多少概率在技能覆盖之下
则:
当内置cd≥覆盖cd时,k=bc/(ac-c+1)
当内置cd<覆盖cd时,k=1-(1-ac/(ac-c+1))*(1-c)^(b-a)
若触发当前轮无法被覆盖到,则将b的值计算时不+1即可
对内置cd≥覆盖cd时的简单不严谨证明:设有N次可判定触发的机会,那么(1-c)N次不触发,cN次触发,而触发一次会有额外(a-1)炮无法触发,所以一共打了(a-1)cN+N=(ac-c+1)N次炮,平均触发率为cN/(ac-c+1)N,而触发一次就覆盖b轮,因此覆盖率为k=bc/(ac-c+1)
证明:设第i轮炮时触发技能的概率为xi
首先我们设a,b≥3,在n较小时寻找规律
则x1=c,x2=c(1-x1)
注意到x1和x2不可能同时发生,即概率独立
因此x3=c(1-x1-x2),而非c(1-x1)(1-x2)
同理立得第a轮炮触发必须前(a-1)轮不触发且该轮触发
任何情况下的递推式为x1=c
xn=c(1-xn-1-xn-2-…-xn-a+1)(n-i均为角标,当i≤0时xi=0)
设发射第i轮炮时正在技能覆盖范围内的概率为ki,则(注意到本轮触发时本轮也可被覆盖)
当b≤a时,
本轮被覆盖当且仅当前b轮中触发一轮,且前几轮概率独立,不可能触发一轮以上
(或者理解成xn的概率不只是概率触发,而是蕴含着必须前(a-1)轮不触发)
因此kn=xn+xn-1+xn-2+…+x(n-b+1)(n-i均为角标,当i≤0时xi=0)
当b>a时,
本轮不被覆盖当且仅当前b轮都不触发,
而这b轮中的前a轮同时不触发的概率为1-∑xi,∑xi为这a轮对应概率之和,因为概率独立
而在概率为(1-∑xi),即前a轮都不触发的情况下,这b轮中的第a+1轮触发概率就是c
同理,在概率为(1-∑xi)(1-c),即前a+1轮都不触发的情况下,第a+2轮的触发概率也就是c
综上1-kn=(1-c)^n(当n≤b-a时)
1-kn=[1-x(n-b+1)-x(n-b+2)-x(n-b+3)-…-x(n-b+a)](1-c)^(b-a)(当n≥b-a时)①
若b轮不包括本轮(即触发当轮不享受buff),则把所有x的角标-1即可
(本段为验证)事实上,易知n≤a时kn都应等于(1-c)^n,下验证此是否与①吻合
易验证x1=c,x2=c(1-c),1-x1-x2=(1-c)^2,符合公式①
易用数学归纳法证明,当n≤a时
x1+x2+…+xn=1-[(1-c)^(n-1)-c(1-c)^(n-1)]=1-(1-c)^n,
xn= c(1-xn-1-xn-2-…-xn-a)=c(1-x1-x2-…-xn-1)=c(1-c)^(n-1)
因此与①吻合
综上我们就得出了任何轮次下的触发概率{xn}和被覆盖概率{kn},如果只想知道某一轮或者前几轮的覆盖概率,直接在{kn}中取用或取前n项平均即可。注意如果是防空炮类间隔式的,需要间隔时间大于内置cd才能用前n轮的算法,否则后面不等于重新开始。
而无穷轮后即递推式中所有的k和x都相等(收敛性证明略),则:
x/c=1-(a-1)x,解得x=c/(ac-c+1)
k=bx(b≤a时)
k=1-(1-ax)*(1-c)^(b-a)(b≥a时)
即得公式
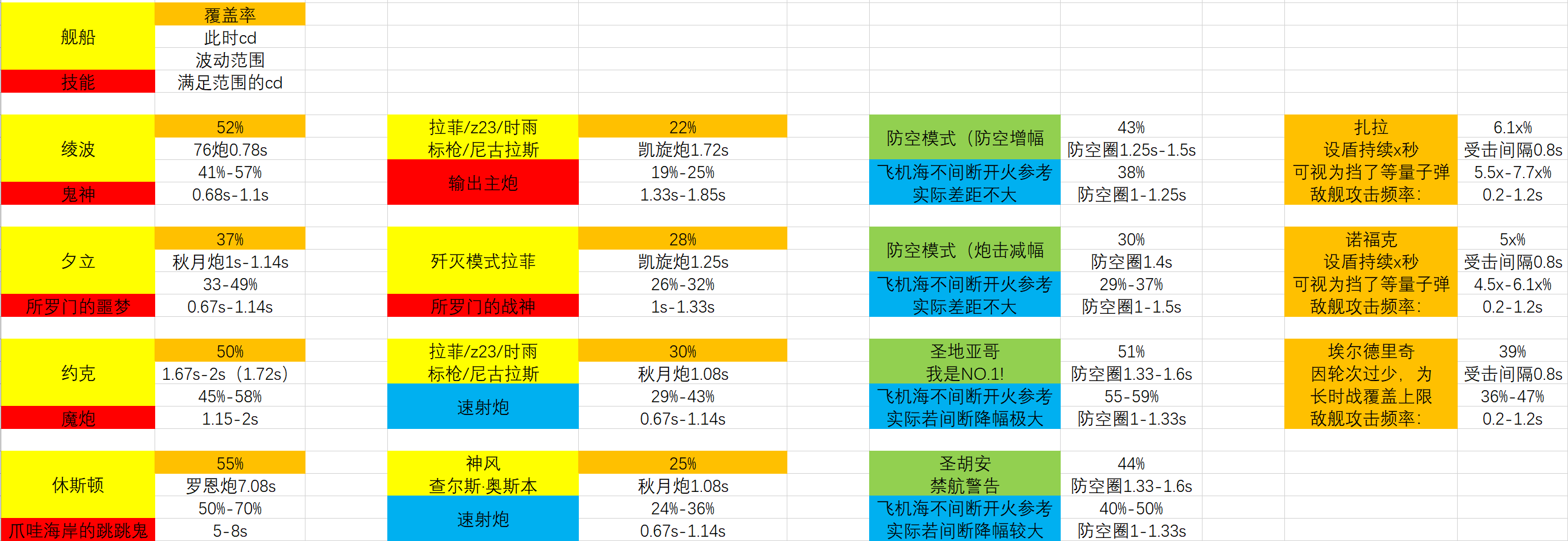
例:内置cd>覆盖cd的例子:
连续飞机海下(防空炮不间断开火),速射金坷垃(防空炮开火间隔在1.33s以内)覆盖率55.26%,正常慢速金坷垃覆盖率51.43%
连续飞机海下,技能【防空模式】正常覆盖率3/7=42.86%,超速射(防空炮开火间隔在1.25s以内)覆盖率37.5%
内置cd<覆盖cd的例子:
计8s5轮炮,5s3轮炮(金凯旋射速1.7-1.8s) ,御三家技能覆盖率为22.06%
拉菲装填提升后射速1.3s,计8s7轮炮,5s4轮炮,则覆盖率为29.17%
若使用紫双联120等方法使射速进1.6s,8s6轮炮,5s4轮炮,则覆盖率为25.45%
其他技能
具体的来说,若此技能与触发技能的炮无关(大部分情况就是增肉技能,但一些主炮触发鱼雷,防空炮触发主炮等,若只关心时间上的覆盖率,不要求精确计算发射时是否卡在时间内,也可使用此情况估计)
也就是你关心的是所有时间段下的平均覆盖情况,则适用此情况
设K为此时无穷轮覆盖率,即无穷轮后在技能覆盖之下的时间占总时长的比例
另外设B=t2/T=持续时间/每轮cd,(不取整+1)
b-B=β
则:
当内置cd≥覆盖cd时,K=Bc/(ac-c+1),
当内置cd<覆盖cd时,K=1-[1-(a-β)c/(ac-c+1)]*(1-c)^(b-a)
对内置cd≥覆盖cd时的简单不严谨证明(同上):设有N次可判定触发的机会,那么(1-c)N次不触发,cN次触发,而触发一次会有额外(a-1)炮无法触发,所以一共打了(a-1)cN+N=(ac-c+1)N次炮,平均触发率为cN/(ac-c+1)N,而触发一次就覆盖B时间,因此覆盖率为k=Bc/(ac-c+1)
证明:设B=持续时间(t)/每轮cd,b-B=β
之前的{kn}实际为某一炮发射时在覆盖期间的概率,
而此时只有两种情况,一种是直到下一炮开火都一直在覆盖时间内(下记两炮之间的“时间段”为“一轮”,炮为时间点)
一种是覆盖此轮的前(1-β)轮就停止,后β轮未被覆盖到
设qn为第n炮和n+1炮之间,只被部分覆盖到(即比整轮少覆盖β轮)的概率
设所求第n炮到n+1炮之间这段时间的平均覆盖率为Kn
则Kn=kn-βqn
而本轮被部分覆盖当且仅当之前第b炮触发,后面全不触发,
类似之前kn的所求过程,当b≤a时,qn=x(n-b+1)
Kn=kn-βqn=xn+x(n-1)+x(n-2)+…+x(n-b+2)+(1-β)x(n-b+1)
无穷轮后K=(b-β)x=Bx
事实上,此时每次触发技能后均覆盖B轮满收益,
因此无穷轮的平均收益仍为k=Bx,只是将b换成B而已。
当b>a时,类似得qn=x(n-b+1)(1-c)^(b-a)(仅n≥b-a时,否则qn=0)
因此Kn=1-(1-c)^n(当n<b-a时)
Kn=1-[1-(1-β)x(n-b+1)-x(n-b+2)-x(n-b+3)-…-x(n-b+a)](1-c)^(b-a)(当n≥b-a时)
无穷轮后K=1-(1-ax+βx)*(1-c)^(b-a)
另外,也可求设任一时间点的被覆盖概率
仍设其为kn(n可取任意实数,n=此时时间/每轮时间+1,即第一轮开炮记为时间轴上点0,和k1)
与之前同理,kn时刻被覆盖当且仅当前B轮时间内至少触发一轮
因此当b≤a时,
kn=x[n]+x[n-1]+x[n-2]+…+x[n-B](除最后一个为向上取整外,[]均为向下取整。当i≤0时xi=0)
当b>a时,
1-kn=(1-c)^n(当n<b-a时)
1-kn=(1-x[n-B]-x[n-B+1]-x[n-B+2]-…-x[n-B+a-1])(1-c)^([n]-[n-B+a-1])(当n≥b-a时,注意除[n]为向下取整外,其他[]均为向上取整)
例:内置cd>覆盖cd的例子:
无限飞机海下,1.5s防空圈射速时,防空模式对炮击的debuff影响覆盖率为2/7=28.57%,1.25射速时为30%,远小于对防空炮的覆盖率,因为触发时也能覆盖到
内置cd<覆盖cd的例子:
绫波主炮0.82s时,覆盖率50.6%
休斯敦若近似视为每两轮底座合计36%触发率,则使用路易炮射速5.33s时,覆盖率66.7%;使用罗恩炮射速7.09s时,覆盖率54.9%
总结
虽然此方法计算的是无穷轮的情况,但证明部分主要算的是有限轮内容,可以算出整个时间轴上每个点的触发率和覆盖率,并不是只能算无穷轮,只不过有限轮时情况繁多,只能展示无穷轮的平均值
实际有限轮的大致情况是,第一轮被覆盖到的概率只有c,第二轮1-(1-c)^2,之后覆盖率会上下波动着迅速增加,迅速逼近求得的k/K,但有限轮的总轮数小于技能每次覆盖轮数b时,一定会离k有很大距离,此时建议用证明中有限轮前期覆盖率来取值计算,例如防空炮只有3轮时,金坷垃覆盖率从51.4%下降至27.1%(未考虑覆盖到下一波飞机的情况);而防空模式因为其对应的b=3,因此覆盖率从42.9%变为42.2%,但仍不是超过。因此k大致可以视为覆盖率的最大值(c<k),且在轮数较多时容易逼近
可用文章先锋舰队投射量与破盾效率最下方的代码模拟验证(本文是以纯数学方法求得)


 沪公网安备 31011002002714 号
沪公网安备 31011002002714 号