科研最优规划理论研究新论
阅读
2023-08-23更新
最新编辑:统合部25000mm装甲附甲
阅读:
更新日期:2023-08-23
最新编辑:统合部25000mm装甲附甲

在线工具
概论
由于能力所限,作者暂时无法解决原有策略中动态策略的分析路线与具体实现。因此,该篇新论将仍然使用前辈研究者所使用的静态科研策略思路。考虑到前辈研究者在研究中的阶段性产生的断层,作者将对以往的研究结论进行一定程度上的总结,并提出新的研究方向。
想要直接快进到结果请戳这里:结果
科研项目统计数据
《新论》将仍然使用前辈所进行的数据结论,即:
军部研究室的内容实质上可分为两类随机事件:(1) 随机刷出5个科研项目;(2)完成科研项目时随机产出。因此,为了对科研策略进行较为准确的评估,首先要进行的工作是对这两类随机事件进行统计。进一步讲,我们关注的是项目的刷出概率与产出期望,这是构建科研策略理论的基石。
内容细节可以参考科研策略专题攻略-科研项目统计与科研五期项目收益与概率统计
理论研究
投入产出计算
《新论》同样使用先前的独立刷新模型,基于同样的刷新概率计算与统计方法,但是对于产出的统计进行了调整。
在原有的算法中,使用的结论为如下:
[math]\displaystyle{ \begin{aligned} &令选取第i个项目的概率为p_i \\ &经过N次科研项目选取(N足够大)后,选取第i个项目的次数为Np_i \\ &设第i个项目的收益为B_i,时长为T_i \\ &则总收益B = \sum_i Np_iB_i,总时长T = \sum_i Np_iT_i \\ &时均收益\beta = \frac{\sum_iNp_iB_i}{\sum_iNp_iT_i} = \frac{\sum_ip_iB_i}{\sum_ip_iT_i} \end{aligned} }[/math]
对于该结论,做出如下调整:
[math]\displaystyle{ \begin{aligned} &仍令选取第i个项目的概率为p_i \\ &设第i个项目的收益为有序数组B_i,时长为T_i \\ &根据原有刷新模型,我们可以得出理论时均收益为有序数组\beta = \frac{\sum_ip_iB_i}{\sum_ip_iT_i} \\ &随后,对该理论收益进行处理。以输入的相关限制和收益单元的参考价值作为约束,我们可以得出一个实数v \\ &则v即是所谓的参考性价比 \end{aligned} }[/math]
《新论》后续的相关算法将会均基于这一参考性价比进行处理与比较。
核心优化-粒子群算法
何为粒子群算法
粒子群优化算法(Particle Swarm Optimization,PSO)是进化计算的一个分支,是一种模拟自然界的生物活动的随机搜索算法。PSO模拟了自然界鸟群捕食和鱼群捕食的过程,通过群体中的协作寻找到问题的全局最优解。
| 鸟群觅食和粒子群优化算法的基本定义对照表 | |
|---|---|
| 鸟群觅食 | 粒子群优化算法 |
| 鸟群 | 搜索空间的一组有效解(表现为种群规模N) |
| 觅食空间 | 问题的搜索空间(表现为维数D) |
| 飞行速度 | 解的速度向量 [math]\displaystyle{ v_i = [v_i^1, v_i^2, ..., v_i^D] }[/math] |
| 所在位置 | 解得位置向量 [math]\displaystyle{ x_i = [x_i^1, x_i^2, ..., x_i^D] }[/math] |
| 个体认知与群体协作 | 每个粒子i根据自身历史最优位置和群体的全局最优位置更新速度和位置 |
| 找到食物 | 算法结束,输出全局最优解 |
在粒子群优化算法中,鸟群中的每个小鸟被称为“粒子”,且同小鸟一样,具有速度和位置。通过随机产生一定数量的粒子作为问题搜索空间的有效解,然后进行迭代搜索,通过该问题对应的适应度函数确定粒子的适应值,得到优化结果。
- 关于粒子群算法不在这里详细展开,如果有时间作者后续会用Manim做一个讲离散粒子群与二进制粒子群的视频。
实际使用中的粒子群算法
将上文所述的粒子群算法应用至该优化问题,我们可以得出如下对应关系:
| 粒子群算法 | 科研规划 |
|---|---|
| 粒子 | 一个规划序列 |
| 粒子的位置向量 | 规划序列本身(有序数组) |
| 最优判断 | 参考性价比 |
因此,实际计算步骤如下:
- 随机生成数个科研序列,作为初始粒子位置(初始化);随机选择其中一个粒子作为初始全局最优解
- 对上述粒子分别计算其性价比,从中选取最高,并与全局最优解进行比较,得出新的全局最优解
- 根据新的全局最优解和粒子本身的历史最优解,对每个粒子更新速度,并进行超额判断,超过速度上限则将其速度减为最大速度的一半
- 根据每个粒子的当前速度,得出新的粒子位置。
- 根据新的粒子位置,得出每个粒子的适应度,并得出历史最优解。
- 重复2~4步,直到达到迭代次数
- 输出结论
其中,粒子本身速度的更新规则如下:
[math]\displaystyle{ v_i^d = \omega \times v_i^d + c_1 \times rand_1^d \times (pBest_i^d - x_i^d) + c_2 \times rand_2^d \times (gBest_i^d - x_i^d) \\ {x_i^d}' = x_i^d + v_i^d }[/math]
而适应度的生成则是根据上文中的参考性价比并进行一定的调整而生成。
算法意义
粒子群算法,作为组合优化问题较新的解决方案,在时间效率和空间效率上都大为超越了前代算法,例如退火算法和决策树,同时其可解释性也超过了如遗传算法等人工智能算法。
并且,粒子群算法作为全局搜索式算法,对于全局最优解具有更加良好的搜寻能力,更不容易陷入局部最优的死结,同时易于使用与改造。
研究结论
桌面应用
概要
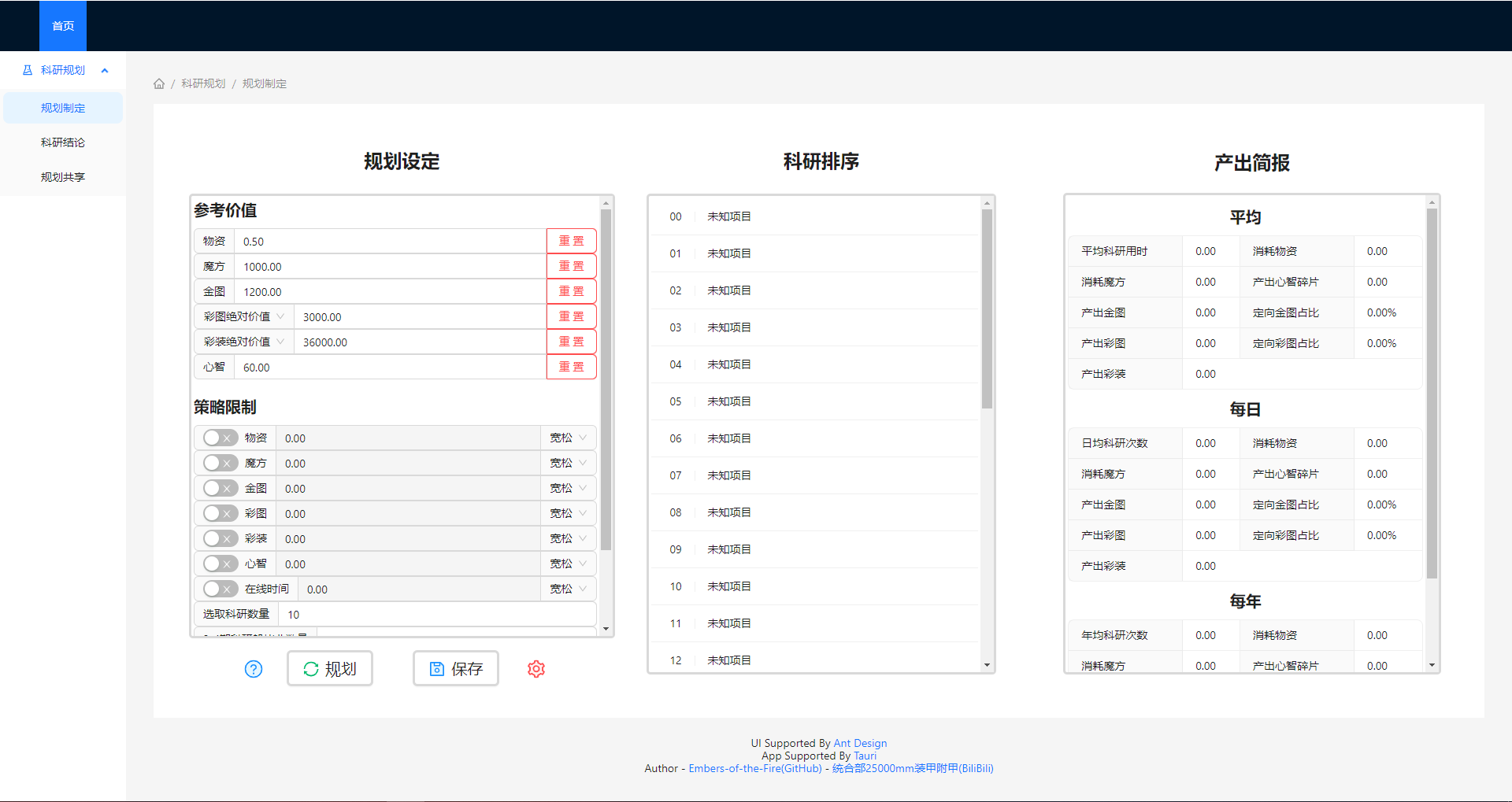
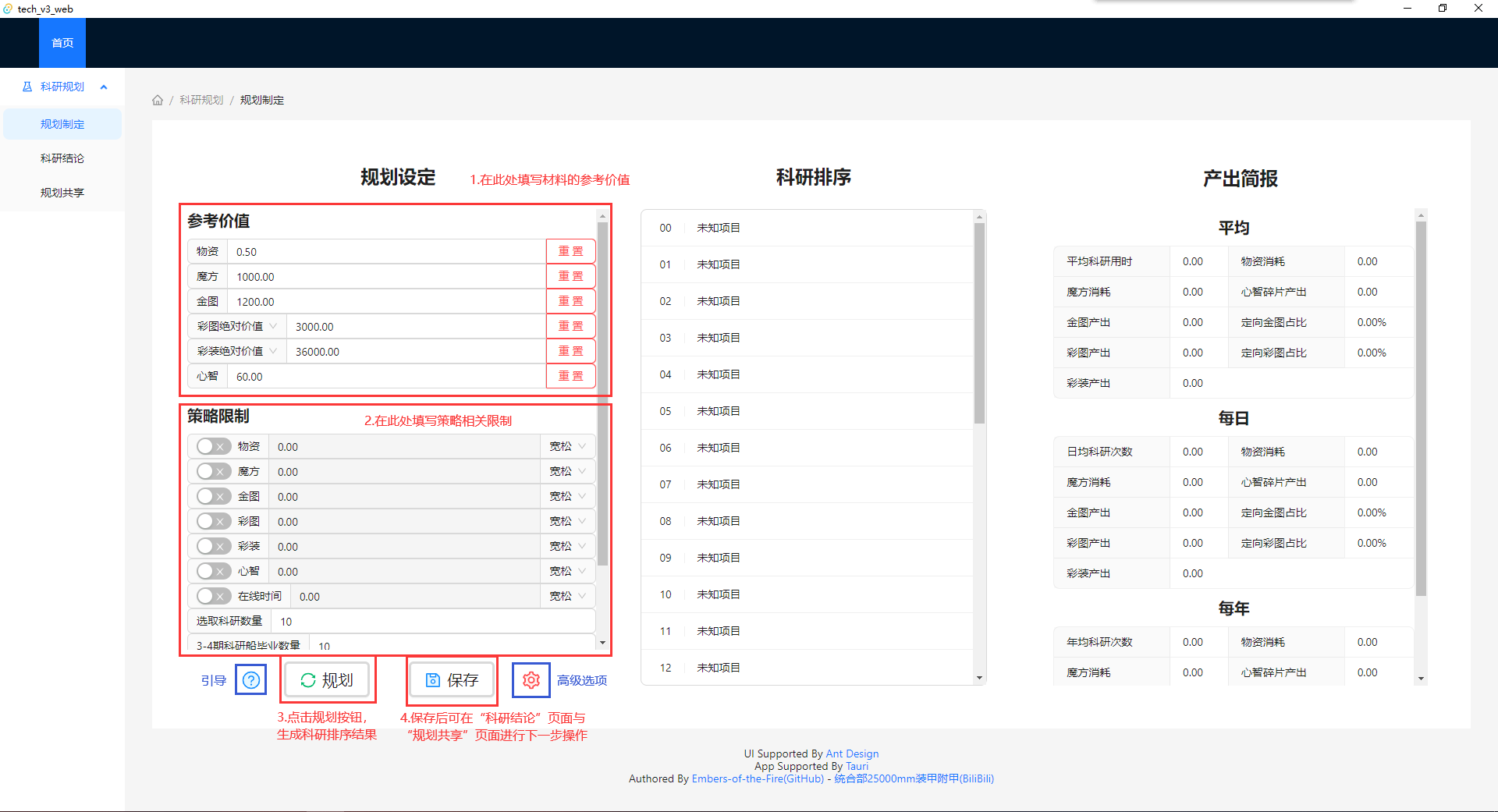
规划制定
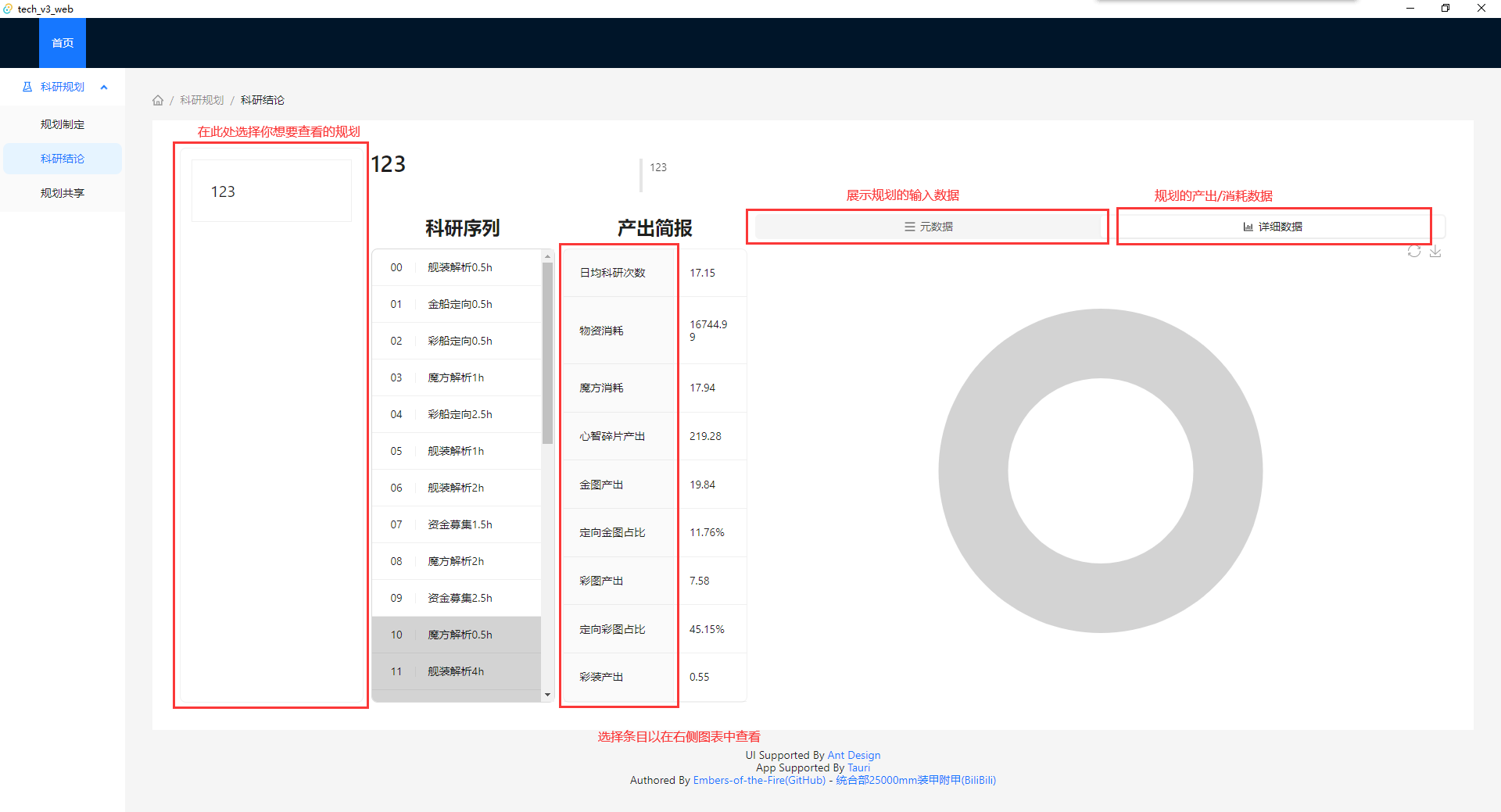
科研结论
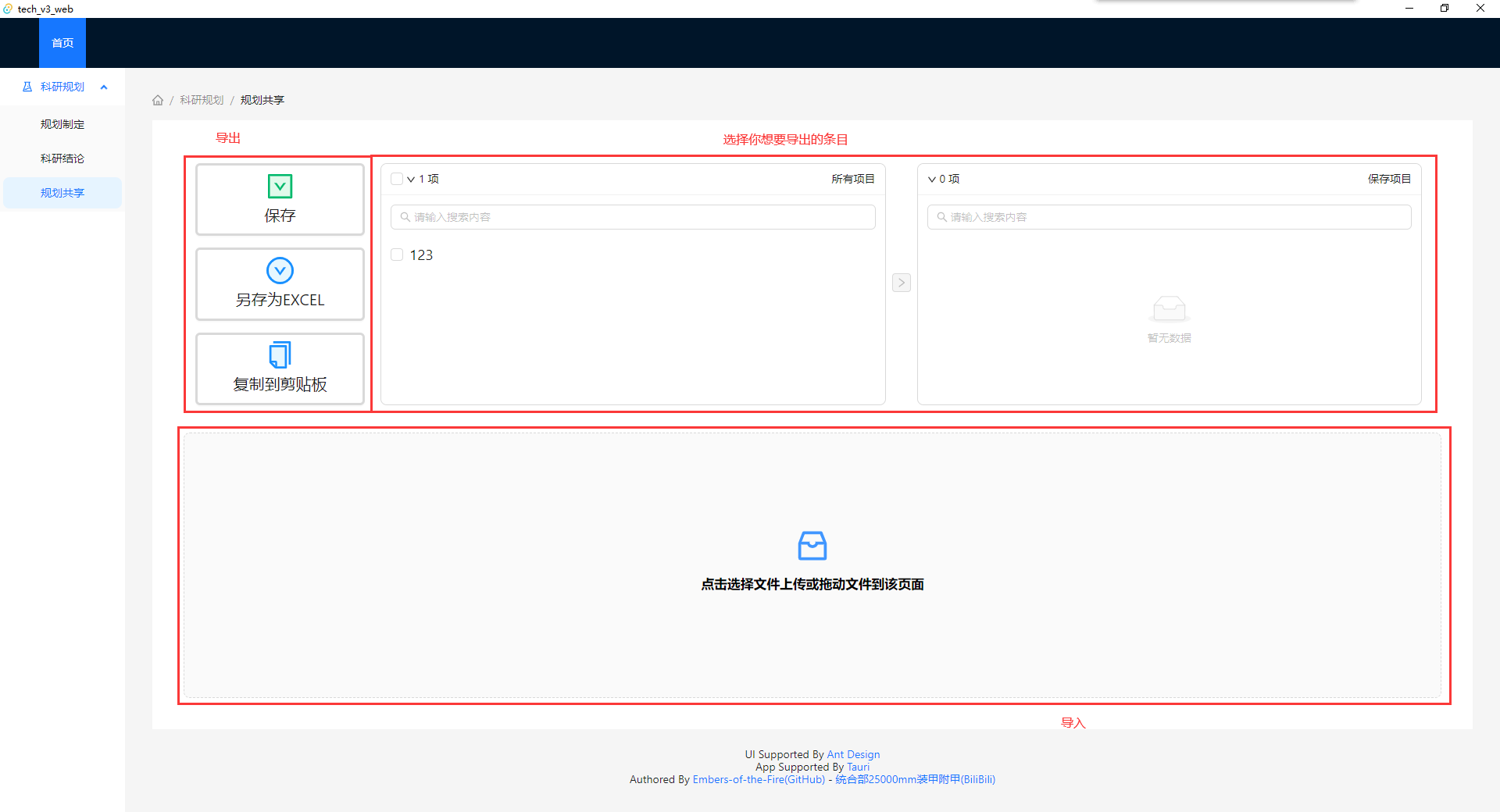
规划共享
百度云链接:百度云
其他事项
- 限于WebView与Tauri的安全策略,保存位置限制为桌面文件夹,且文件名为自动生成
- 导入文件无目录限制,可以同时多选拖入


 沪公网安备 31011002002714 号
沪公网安备 31011002002714 号