跨射炮弹的散布模型
阅读
2020-12-23更新
最新编辑:Leo丶莱茵
阅读：
更新日期：2020-12-23
最新编辑：Leo丶莱茵
本文原文见B站专栏文章：（碧蓝航线的跨射炮弹散布模型【可视化航线第0期(demo)】），(可能更加靠谱的碧蓝航线的跨射炮弹散布模型【可视化航线第1期】)，由原文作者整理、汇编。
前言
作为当前版本的推图主力（大概不需要之一），后排大炮的主炮输出显然直接影响着整支队伍的强度。在相当大的程度上，战列、战巡的主炮输出受到主炮装备面板数值的影响，而其中炮弹散布的影响往往是比较难以量化的。随着一系列降低散布机制的上线（
厌战改、
98式复读机、
乔五），当前碧蓝版本的后排主炮配装需要考虑到散布值降低对输出提升的影响。在这里，我假设了两种不同的跨射炮弹散布模型，对固定靶进行射击模拟，统计了不同主炮的单轮射击命中数与散布降低值之间的关系。在这两个模型下，我们可以得到的基本结论如下：
1. 模型概述： 第一种模型（高斯模型）的最大散布圈为椭圆型，散布圈内炮弹按二维高斯函数分布；第二种模型（风阻模型）参考了wiki上命中与BB的不寻常关系一文，最大散布圈的形状接近于400m跑道的样子，散布圈内炮弹的分布为两种均匀分布的概率函数的叠加（最终炮弹的落点并不是均匀的）。
2. 通过模型计算出的主炮命中率： 两种散布模型下，对单一固定靶进行主炮射击，
MK6的单颗子弹命中率约为78.7%（高斯模型）/74.1%（风阻模型），
410的单颗子弹命中率约为87.1%（高斯模型）/84.1%（风阻模型）。作为对比，前排舰船炮击输出性价比和生存性价比 粗量化比较中提到的MK6命中率为72%，410命中率为83%，故风阻模型可能与实战结论更为接近。
3. 减散布收益： 在一定范围内，跨射主炮对固定靶的物理命中率和散布降低值可以近似为线性关系。在两种模型的线性范围内，每减1点散布约相当于提高约4%单轮主炮物理命中数，其中高斯模型给出的预期收益略高于风阻模型：厌战改在主炮散布减5并使用MK6时，对固定靶进行射击，物理命中率相较于不减散布时提升了22%（高斯模型）/20%（风阻模型）。
4. 减散布收益的线性域： （1）高斯模型中，偏离上述线性关系所需的散布减少量与主炮面板散布有关：紫410mm约在散布-4时偏离，MK6约在散布-6时偏离。散布减少量超过这个阈值后，减散布所带来的物理命中率提高的收益降低。 （2）风阻模型中，上述线性关系范围很大，在减0~7点面板散布的范围内，MK6、410、四联356均为出现任何明显的阈值。（3）对于这两种模型，当减掉的面板散布大时，410的减散布收益均明显低于MK6和
四联356。
5. 复读机的收益： 两种模型下，对于炮击值600（面板+装备）的后排战列舰，携带复读机的收益（主炮输出期望约+12.9%）均低于
黑弹（约+14.4%），这与当前的一些实测（如九八式延迟射击装置13-4道中对比超重弹弹链的收益测试）结论一致。
请注意：
1. 由于作者并没有看过碧蓝航线的代码，所以本文中的理论模型、结论推论可能与实战数据存在较大差异。这篇文章只是我和舰队里的秃子讨论之后心血来潮写的一份推测，不代表真正的游戏机制，更不代表实际作战。作者欢迎各种类型的模型讨论和实战检测。
2. 本文原文使用Jupyter Notebook上的markdown语言写作，代码为Python 3，有条件的读者应该可以执行代码，完成结论重现。由于本文作者所受过的编程培训实在有限，代码写作的规范性可能引起您的不适，请酌情无视。如果不想看代码，直接无视掉程序框内的所有内容即可（已折叠）。
3. 本文的主炮原始数据来源于wiki上玄虚小圣的跨射炮弹和跨射弹幕细节数据一览，第二种模型（风阻）的思路来源于命中与BB的不寻常关系（虽然我对这篇文章中的部分细节有些怀疑），同时我也阅读了wiki上炮姐爱喝柠檬汁的随版本更新的装备解析，这几篇文章对我的建模有很大的帮助。同时向之前几位给过我意见和建议的大佬们表示感谢（毕竟我只是一个连红染碑都没有的小萌新）。
建立主炮的物理模型
首先，我们先导入以下python模块，以便进行接下来的科学计算和绘图。
import numpy as np
from matplotlib import pyplot as plt
from matplotlib import patches
plt.rcParams.update({'font.size': 18})
plt.rcParams['font.sans-serif'] = ['Adobe Heiti Std'] # 用来正常显示中文
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
接着，让我们来建立主炮的物理模型。在这里，我定义了一个叫Gun()的对象，用来代表各种主炮，它包含了我们需要的主炮面板信息。这其中最主要的信息有：
1. 单轮主炮弹数（Gun.shell_num），比如MK6是3，410是2。
2. 着弹范围（ Gun.aoe_area），我将这个量理解为了单颗炮弹的AOE圈半径，换言之，距离靶心小于这一值的炮弹都算物理命中，当然实际命中还要考虑闪避公式。对于绝大部分后排跨射主炮，这一值为15（引用自小圣的表格）。注意：在这个表格中，我把所有的距离量都理解为了半径，如散布22，我理解成了最大散布圈的半径。统一理解为半径和统一理解为直径的结论是一致的。
接下来我所定义的变量在高斯模型和风阻模型中有所区别，我们分别讨论：
高斯模型
3. 面板散布范围（Gun.dispersion），我的理解是水平方向的炮弹最大散布圈半径。也就是说，瞄准固定靶射击，水平方向着弹点距离靶心距离不会超过这个值。典型地，MK6的散布是22。
4. XZ偏移（Gun.xz_shift）我在这里理解为了竖直方向的炮弹最大散布圈半径。也就是说，炮弹的散布圈是个椭圆，椭圆方程为:
(x - x_0)^2 / (Gun.dispersion)^2 + (y - y_0)^2 / (Gun.xz_shift)^2 = 1
其中(x,y)是炮弹落点， (x_0, y_0)是瞄准的靶心。任何炮弹的落点不会超过这个椭圆。据舰队里的某位匿名老干tu部zi体感，手机横屏方向的炮弹散布要比竖直方向大，大概说的就是XZ偏移要略小于散布范围。典型地，MK6的XZ偏移是19。
5. Sigma（Gun.sigma），这个值是我随便添加的，目前取1。我们可以假设着弹点的二维分布是高斯的，也就是说，对于单一一颗炮弹，其落点相对于靶心的方位角Θ是完全随机的，落点与靶心的位移r满足高斯分布：
P(r)= 1 / [σ√(2π)] × e^(- 1/2 × r^2 / σ^2), r ∈ (-∞, +∞)
其中P(r)是落点距靶心r的概率，满足归一化条件：
∫_{-∞}^{+∞} P(r) dr = 1
但由于最大散布圈的存在，我们规定r不得超过一个上限，在水平方向上这个上限是Gun.dispersion，竖直方向上是Gun.xz_shift，其他方向上用勾股计算，我们取这一上限为r_{max}。正因如此，我们规定高斯分布的标准差σ为：
σ = r_{max}/ Gun.sigma
同时新的散布距离为r ∈ [-r_{max}, +r_{max}]，新的概率分布函数Q(r)=c × P(r)为原来函数的c倍, 满足新的归一化条件∫_{-r_{max}}^{+r_{max}} Q(r) dr = 1 。这样，每一发炮弹的落点均可以用这个概率模型表达出来，剩下的事情就可以交给程序了：通过生成随机数，来模拟主炮的落点，判断是否能够命中靶心。
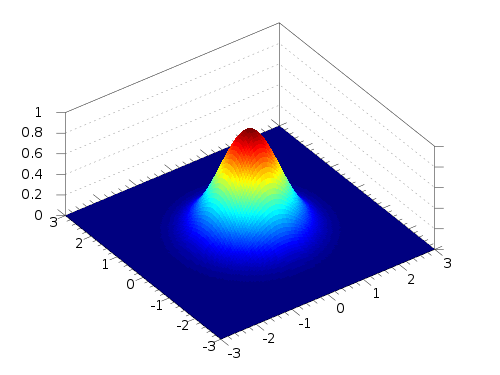
下图表示了二维高斯分布的样子，来源为英文维基Gaussian funtion词条：
在进行减n点散布的时候，我用了下述公式：
1. 水平散布： 直接减就行，也就是：
Gun.dispersion_新 = Gun.dispersion_旧 - n
2. 竖直散布： 减量要通过竖直/水平比来调整，也就是：
Gun.xz_shift_新 = Gun.xz_shift_旧 × (1 - n / Gun.dispersion_旧)
风阻模型
上面的高斯模型是我一开始建模时想出来的模型，似乎wows里面的炮弹散布模型类似于这个（我是wows云玩家）。经过高人指点批评教育，外加更仔细地阅读了一点资料（主要是命中与BB的不寻常关系），我发现上面里提到的椭圆的、高斯分布的散布模型可能是不对的（虽然最后得到的一些结论似乎还是站得住脚的）。在新的模型下，一门后排跨射主炮 Gun() 的散布模型应有以下几个重要参数：
3. 面板散布范围 (Gun.dispersion)，在新模型下，这一个面板散布范围变成了类似评分项的东西，面板散布不直接影响真正的散布圈大小。真正的散布圈大小由下面这个的量控制：
4. XZ偏移 (Gun.dispersion)，这个量在新模型中代表原始散布圈的半径，如MK6是19。我也是经过高人指点才知道，这里的XZ平面实际上指的是海平面，Y轴才是垂直海平面的那个轴，所以XZ偏移说的就是炮弹落点到靶心的最大偏移。但是，由于接下来要讲的参数的控制，在这里XZ偏移只代表竖直方向的最大散布距离。多说一句，我这里说的竖直方向就是手机横屏肝图后，短边的那个方向。
5. 随机偏移 （有一种叫法叫风阻偏移 ），大概说的是炮弹沿着水平方向射出之后，由于风阻的存在导致的水平方向的落点偏移，在命中与BB的不寻常关系一文中，这一值取为了（-10， 10）之间随机均匀分布的补正，这个数不影响竖直方向的偏移。综上，通过沿用这个10点的随机偏移（虽然我不知道这个数的来源是哪里），我们大概可以如下计算炮弹落点：
在进行减散布的时候，由于减掉的依然是面板散布，而非实际的XZ偏移，所以我们要通过面板散布来进行放缩，从而得到新的竖直方向最大散布距离。公式和上一次是一致的：
Gun.xz_shift_新 = Gun.xz_shift_旧 × (1 - n / Gun.dispersion_旧)
接下来，就让我们在主炮对象Gun()下，根据上述定义的物理模型，定义一些随机开n炮、判断命中、绘制散布圈的函数吧：
# 定义对象： 主炮
class Gun:
def __init__(self, name = '406mm_mk6', # 炮名
shell_type = 'HE', # 弹种 （暂时没用上）
shell_num = 3, # 弹数
damage_per_shell = 156, # 强满单发伤害
period = 24.02, # 强满面板射速 (s)
compensation = 1.05, # 舰炮补正（注意不是护甲补正）
sigma = 1, # 二维高斯散布的sigma
speed = 10, # 弹速 （暂时没用上）
aoe_area = 15, # 着弹范围 （AOE圈半径）
xz_shift = 19, # XZ偏移 （我理解为了竖直方向散布）
dispersion = 22, # 散布范围 （我理解为了水平方向散布）
):
self.name = name
self.shell_type = shell_type
self.shell_num = shell_num
self.damage_per_shell = damage_per_shell
self.period = period
self.compensation = compensation
self.sigma = sigma
self.speed = speed
self.aoe_area = aoe_area
self.xz_shift = xz_shift
self.dispersion = dispersion
# 假设炮弹的落点是在最大散布圈(dispersion，散布圈半径)内高斯分布，
# 最大散布圈相当于高斯分布标准差的sigma倍
def shoot_one_shell(self): # 打一发主炮
tmp_theta = np.random.rand(1)*np.pi*2 # 椭圆参数角
tmp_pa = np.arctan(self.xz_shift/self.dispersion * np.tan(tmp_theta)) #椭圆方位角
tmp_max_r = np.sqrt((self.dispersion*np.cos(tmp_theta))**2 + (self.xz_shift*np.sin(tmp_theta))**2)
tmp_r = np.random.normal(loc = 0, scale = tmp_max_r / self.sigma)
while np.abs(tmp_r) > tmp_max_r:
tmp_r = np.random.normal(loc = 0, scale = tmp_max_r / self.sigma)
tmp_x, tmp_y = np.cos(tmp_pa) * tmp_r, np.sin(tmp_pa) * tmp_r
return (tmp_x, tmp_y)
def shoot_one_round(self): # 打一轮主炮, 即shell_num发
tmp_theta = np.random.rand(self.shell_num)*np.pi*2 # 椭圆参数角
tmp_pa = np.arctan(self.xz_shift/self.dispersion * np.tan(tmp_theta)) #椭圆方位角
tmp_max_r = np.sqrt((self.dispersion*np.cos(tmp_theta))**2 + (self.xz_shift*np.sin(tmp_theta))**2)
tmp_r = np.random.normal(loc = 0, scale = tmp_max_r / self.sigma)
while np.sum(np.abs(tmp_r) > tmp_max_r) > 0:
arg_out = np.where(np.abs(tmp_r) > tmp_max_r)
tmp_r[arg_out] = np.random.normal(loc = 0, scale = tmp_max_r[arg_out] / self.sigma)
tmp_x, tmp_y = np.cos(tmp_pa) * tmp_r, np.sin(tmp_pa) * tmp_r
return (tmp_x, tmp_y)
def shoot_n_round(self, n): # 打n轮主炮, 即shell_num * n发
tmp_theta = np.random.rand(self.shell_num * n)*np.pi*2 # positional angle
tmp_pa = np.arctan(self.xz_shift/self.dispersion * np.tan(tmp_theta)) #椭圆方位角
tmp_max_r = np.sqrt((self.dispersion*np.cos(tmp_theta))**2 + (self.xz_shift*np.sin(tmp_theta))**2)
tmp_r = np.random.normal(loc = 0, scale = tmp_max_r / self.sigma)
while np.sum(np.abs(tmp_r) > tmp_max_r) > 0:
arg_out = np.where(np.abs(tmp_r) > tmp_max_r)
tmp_r[arg_out] = np.random.normal(loc = 0, scale = tmp_max_r[arg_out] / self.sigma)
tmp_x, tmp_y = np.cos(tmp_pa) * tmp_r, np.sin(tmp_pa) * tmp_r
return (tmp_x, tmp_y)
def shoot_n_round_windy(self, n): # 打n轮主炮, 即shell_num * n发, 选用风阻模型，风阻随机参量为10
tmp_pa = np.random.rand(self.shell_num * n) * 2 * np.pi
tmp_r = np.random.rand(self.shell_num * n) * self.xz_shift
wind_shift = np.random.uniform(-10, 10, self.shell_num * n)
tmp_x = wind_shift + np.cos(tmp_pa) * tmp_r
tmp_y = np.sin(tmp_pa) * tmp_r
return (tmp_x, tmp_y)
def center_hit_per_round(self, n=1, norm = True): # 打一轮主炮，命中中心多少发？
if norm == True: # 使用正态分布模型
hit_pos = self.shoot_n_round(n)
else: # 使用风阻模型
hit_pos = self.shoot_n_round_windy(n)
return np.sum(np.sqrt(np.sum(np.square(hit_pos), axis = 0)) < self.aoe_area)/n
def draw_dispersion_range(self, **kwargs): #画出散布圈 （高斯模型）
dsp_patch = patches.Ellipse(xy = (0,0) ,
width = self.dispersion*2, height = self.xz_shift*2, **kwargs)
plt.gca().add_patch(dsp_patch)
def draw_dispersion_range_windy(self, **kwargs): #画出散布圈 (风阻模型)
left_patch = patches.Arc(xy = (-10, 0) ,
width = self.xz_shift*2, height = self.xz_shift*2,
theta1=90.0, theta2=270.0, **kwargs)
right_patch = patches.Arc(xy = (+10, 0) ,
width = self.xz_shift*2, height = self.xz_shift*2,
theta1=270.0, theta2=90.0, **kwargs)
con_top = patches.ConnectionPatch((-10, self.xz_shift), (10, self.xz_shift),
coordsA="data", coordsB="data", **kwargs)
con_bot = patches.ConnectionPatch((-10, -self.xz_shift), (10, -self.xz_shift),
coordsA="data", coordsB="data", **kwargs)
plt.gca().add_patch(left_patch)
plt.gca().add_patch(right_patch)
plt.gca().add_patch(con_top)
plt.gca().add_patch(con_bot)
利用上面的Gun()对象， 我们初始化以下四门主炮：美式406mm MK6（MK6，us_mk6），日式410mm连装炮（410，jp_410），英式356mm四联装炮（大哥炮，uk_356），以及厌战改装备MK6的特殊情况（ws_mk6， ws就是Warspite哇死白头了）
us_mk6 = Gun(name = '406mm_mk6', shell_num = 3, damage_per_shell = 156, compensation = 1.05, period = 24.02,
xz_shift = 19, dispersion = 22)
jp_410 = Gun(name = '410mm_twin', shell_num = 2, damage_per_shell = 154, compensation = 1.10, period = 20.02,
xz_shift = 16, dispersion = 20)
uk_356 = Gun(name = '356mm_quad', shell_num = 4, damage_per_shell = 108, compensation = 1.05, period = 29.19,
xz_shift = 19, dispersion = 25)
ws_mk6 = Gun(name = '406mm_mk6', shell_num = 3, damage_per_shell = 156, compensation = 1.00, period = 24.02,
xz_shift = 19*(22-5)/22, dispersion = 22-5)
炮弹落点散布圈的可视化
在我们计算主炮的物理命中率、减散布的收益之前，让我们来先可视化一下上述定义的四门主炮的散布圈。我们让四门主炮分别进行500轮固定靶射击，假设固定靶位于坐标原点(0, 0)，射击结果由下述代码模拟/绘制：
plt.figure(figsize = (8,8))
# 瞄准(0,0)
plt.axhline(0, ls ='--', color ='grey', lw =2)
plt.axvline(0, ls ='--', color ='grey', lw =2)
# 射击轮次
shoot_round = 500
# 美帝妹控6
x, y = us_mk6.shoot_n_round(shoot_round)
plt.scatter(x, y, color= 'b', marker = '.', label = '406mm MK6', alpha = 0.5)
us_mk6.draw_dispersion_range(ec = 'b', fc = 'none', lw = 1.2)
# 本子410
x, y = jp_410.shoot_n_round(shoot_round)
plt.scatter(x, y, color= 'r', marker = '.', label = '410mm连装炮', alpha = 0.5)
jp_410.draw_dispersion_range(ec = 'r', ls = '-', fc = 'none', lw =1.0)
# 英吹356
x, y = uk_356.shoot_n_round(shoot_round)
plt.scatter(x, y, color= 'g', marker = '.', label = '四连装356mm', alpha = 0.5)
uk_356.draw_dispersion_range(ec = 'g', ls = ':', fc = 'none', lw =2)
# 厌战mk6
x, y = ws_mk6.shoot_n_round(shoot_round)
plt.scatter(x, y, color= 'k', marker = '.', label = '406mm MK6（厌战）', alpha = 0.45)
ws_mk6.draw_dispersion_range(ec = 'k', ls = '--', fc = 'none', lw =2)
# 物理命中区域
dsp_patch = patches.Ellipse(xy = (0,0) ,
width = 15*2, height = 15*2, color = 'grey', alpha = 0.35,
label = '物理命中范围 (15)')
plt.gca().add_patch(dsp_patch)
# 绘制图例等
plt.legend(framealpha = 0.8, loc = 4,
ncol = 2, handletextpad = 0.5, columnspacing = 0.2)
plt.gca().set(aspect = 1, xlim = (-30, 30), ylim = (-30, 30),
xlabel = '水平偏移', ylabel='竖直偏移',
title = '%d轮主炮射击固定靶的散布圈示意 （高斯模型）'%shoot_round)
plt.tight_layout()
plt.savefig('disp_散布圈示意图.jpg', dpi = 150)
绘制结果如下：
| 高斯模型 | 风阻模型 |
|---|---|
|
|
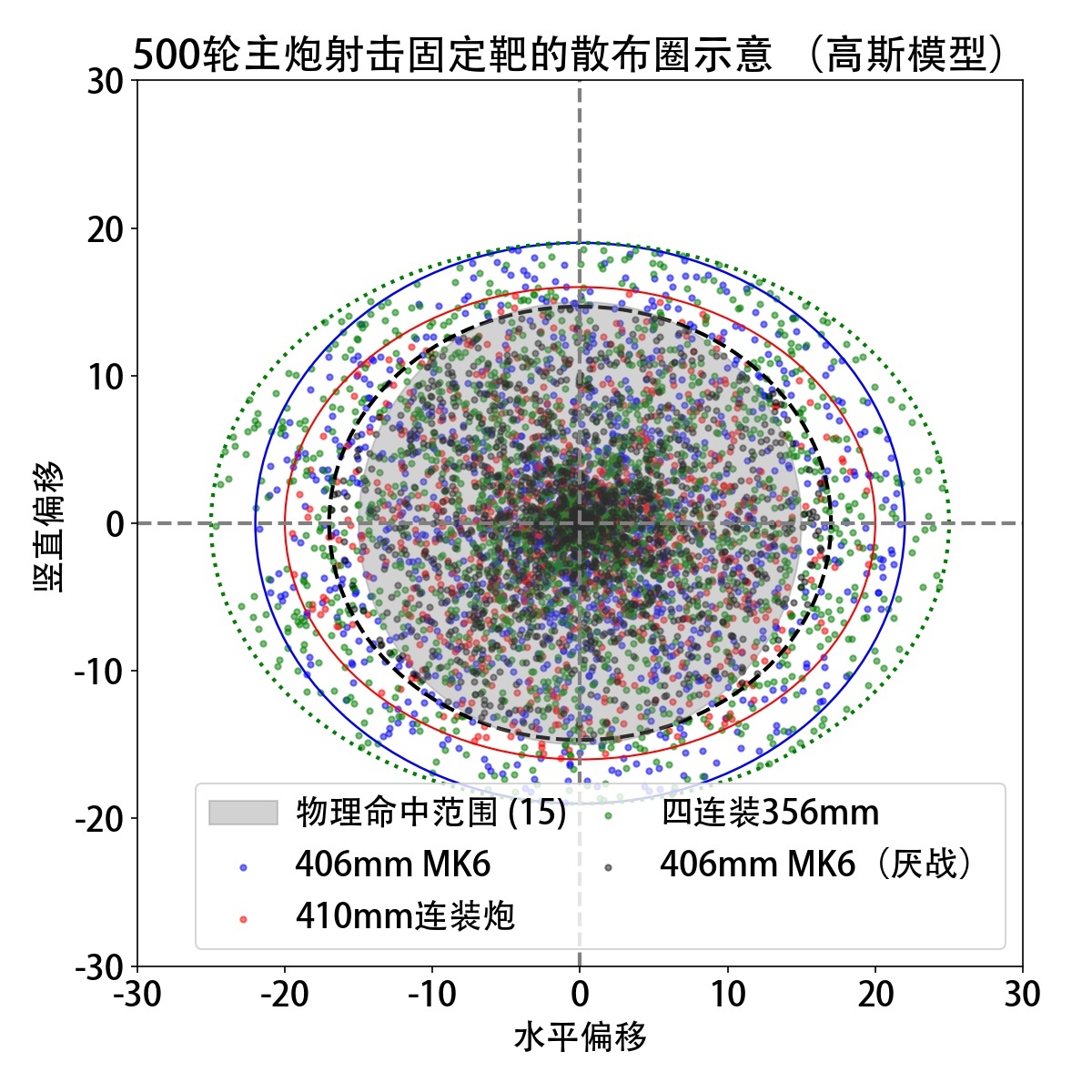
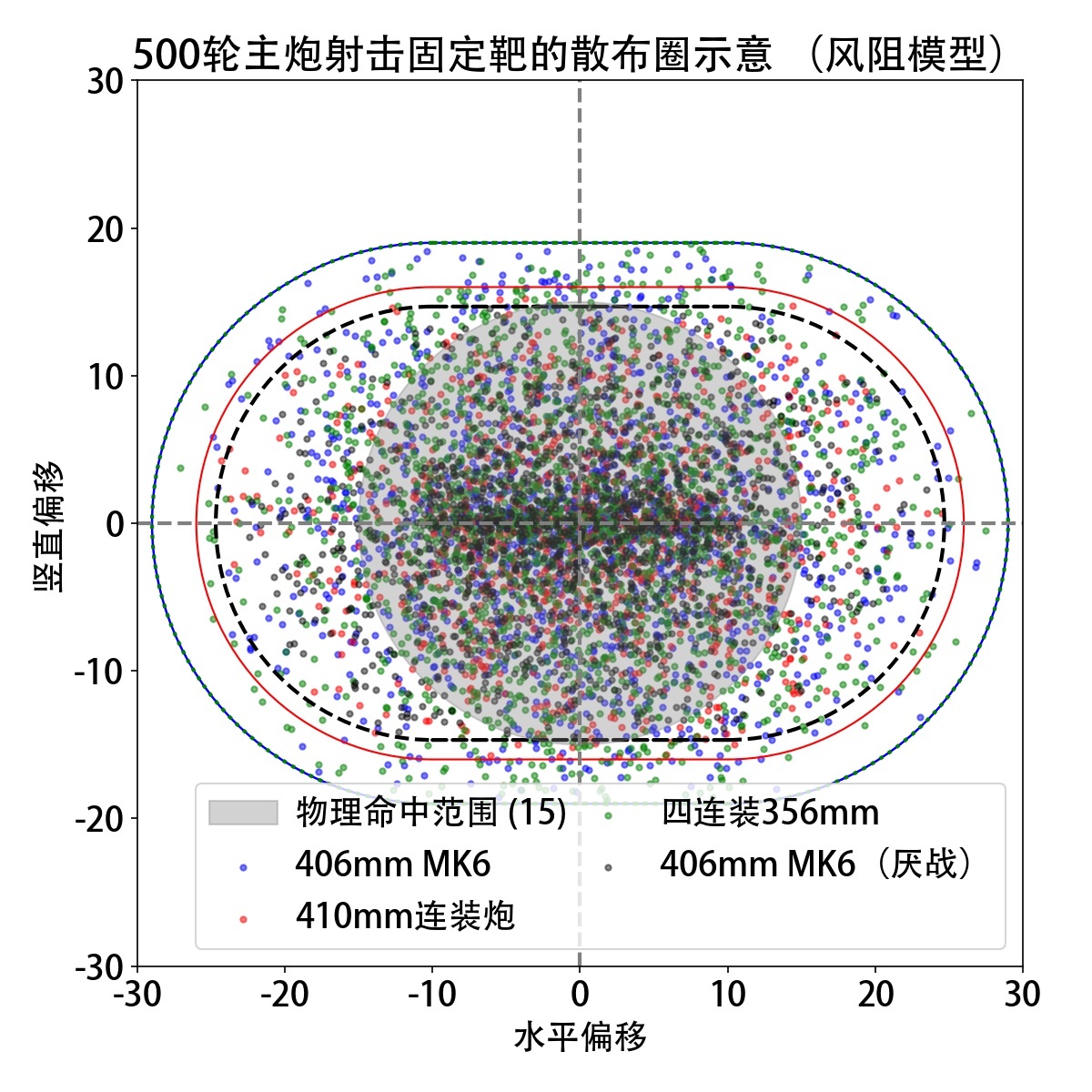
绘制结果就是上面的两张图了，每一发炮弹的落点已用不同色的小圆点标识（见图例），每一种主炮的散布圈也用对应颜色的图形标记了出来。
在高斯模型中，散布圈是椭圆的，我们都知道主炮子弹数越多，散布圈越大，所以散布圈的大小顺序为四联356>MK6>410。物理命中圈由灰色阴影区标记——我们可以看见一件很恐怖的事情：厌战改的散布圈基本跟物理命中范围重合，这也就给了厌战改对固定靶极高的物理命中率然而这不见得是对的，至少可能没这么恐怖。
在风阻模型中，散布圈形状是两头圆中间平的，很像400米的标准跑道。实际上，虽然我们在XZ偏移、风阻偏移这两个量中都取了均匀分布的模型，实际炮弹的落点看起来还是更偏向与中间的，能落在极端的左右两头的概率看起来也确实不高。与高斯模型相比，厌战改的物理命中率似乎没那么高了。
我们可以统计两种模型中炮弹落点的径向分布，并加以对比。这里以MK6为例：
x, y = us_mk6.shoot_n_round_windy(10000)
distance_windy = (x**2 + y**2)**0.5
x, y = us_mk6.shoot_n_round(10000)
distance_gauss = (x**2 + y**2)**0.5
bins = np.arange(-1, 26, 1.0)
bins_n_windy, bins_e = np.histogram(distance_windy, bins = bins)
bins_n_gauss, bins_e = np.histogram(distance_gauss, bins = bins)
bins_c = (bins_e[1:] + bins_e[:-1])/2.
plt.close()
plt.figure(figsize = (8,5))
plt.step(bins_c, bins_n_gauss, where = 'mid', lw = 4, label = '高斯椭圆模型 (Sigma=1)')
plt.step(bins_c, bins_n_windy, where = 'mid', lw = 4, label = '风阻模型 (最大偏移=10)')
plt.axvline(19, 0.7, 0.85, lw = 2, c ='k')
plt.text(19, 0.86*2.1e3, 'XZ偏移', va ='bottom', ha = 'center')
plt.legend()
plt.gca().set(xlim = (0, 25), ylim = (0, 2.1e3),
xlabel = '炮弹落点到靶心的距离', ylabel = '单位距离内散落的炮弹数量',
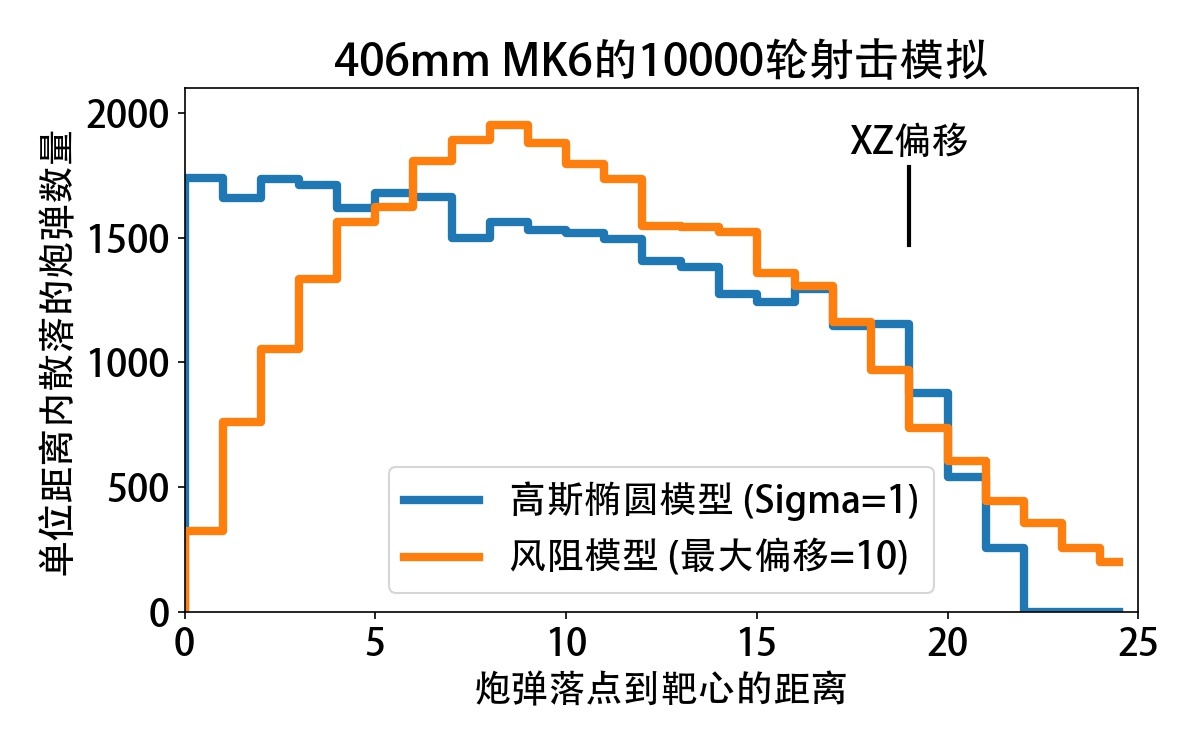
title = '406mm MK6的10000轮射击模拟')
plt.tight_layout()
plt.savefig('disp_模型对比.jpg', dpi = 150)
也就是说，对于MK6这门主炮，高斯模型下（蓝色），打在靶心的概率要高于其他的距离处，这确实是高斯分布的特征，中心概率最大；而风阻模型（橙色）下，炮弹打到距离8-10的概率要更大一些，稳稳10环命中靶心的概率比较小。这可能说明风阻模型跟实战更为接近——个人感觉，跨射炮弹稳稳砸中目标似乎是一件不太容易的事情，稍稍偏一点的概率更高。高斯模型中，打在距离靶心5格内的次数要明显高于风阻模型，我觉得实战还是有能力检验这个事情的（比如统计0-5和5-10之间的次数比值，来至少排除其中一个模型），所以欢迎读者反馈你的实战感受。
单轮主炮射击的物理命中数期望
接下来，我们让每个主炮射击10000次， 来统计平均每轮主炮的命中数，计算不同主炮、不同散布参数下的主炮射击固定靶的命中率：
# 物理命中数
phy_hit_per_round = np.array([us_mk6.center_hit_per_round(10000, norm = True),
jp_410.center_hit_per_round(10000, norm = True),
uk_356.center_hit_per_round(10000, norm = True),
ws_mk6.center_hit_per_round(10000, norm = True), ])
# 实际炮弹数
tot_hit_per_round = np.array([us_mk6.shell_num,
jp_410.shell_num,
uk_356.shell_num,
ws_mk6.shell_num])
# 物理命中率
hit_rate = phy_hit_per_round / tot_hit_per_round * 100
# 棒状图绘图参数：
ind = np.arange(4) # the x locations for the groups
width = 0.35 # the width of the bars
fig, ax = plt.subplots(1,1, figsize = (10,6))
rects1 = ax.bar(ind - width/2, phy_hit_per_round, width,
label='固定靶物理命中数')
rects2 = ax.bar(ind + width/2, tot_hit_per_round, width,
label='发射炮弹数')
# ax.set_yticks(np.arange(0,5))
ax.set_xticks(ind)
ax.set_xticklabels(['406mm MK6\n%.1f%%'%(hit_rate[0]),
'410mm连装炮\n%.1f%%'%(hit_rate[1]),
'四联装356mm\n%.1f%%'%(hit_rate[2]),
'厌战MK6\n%.1f%%'%(hit_rate[3])])
ax.set_ylabel('单轮主炮的炮弹数目')
ax.set_title('高斯模型（Sigma=1）')
ax.legend(loc=4, framealpha = 0.9)
plt.tight_layout()
plt.savefig('disp_固定靶命中率.jpg', dpi = 150)
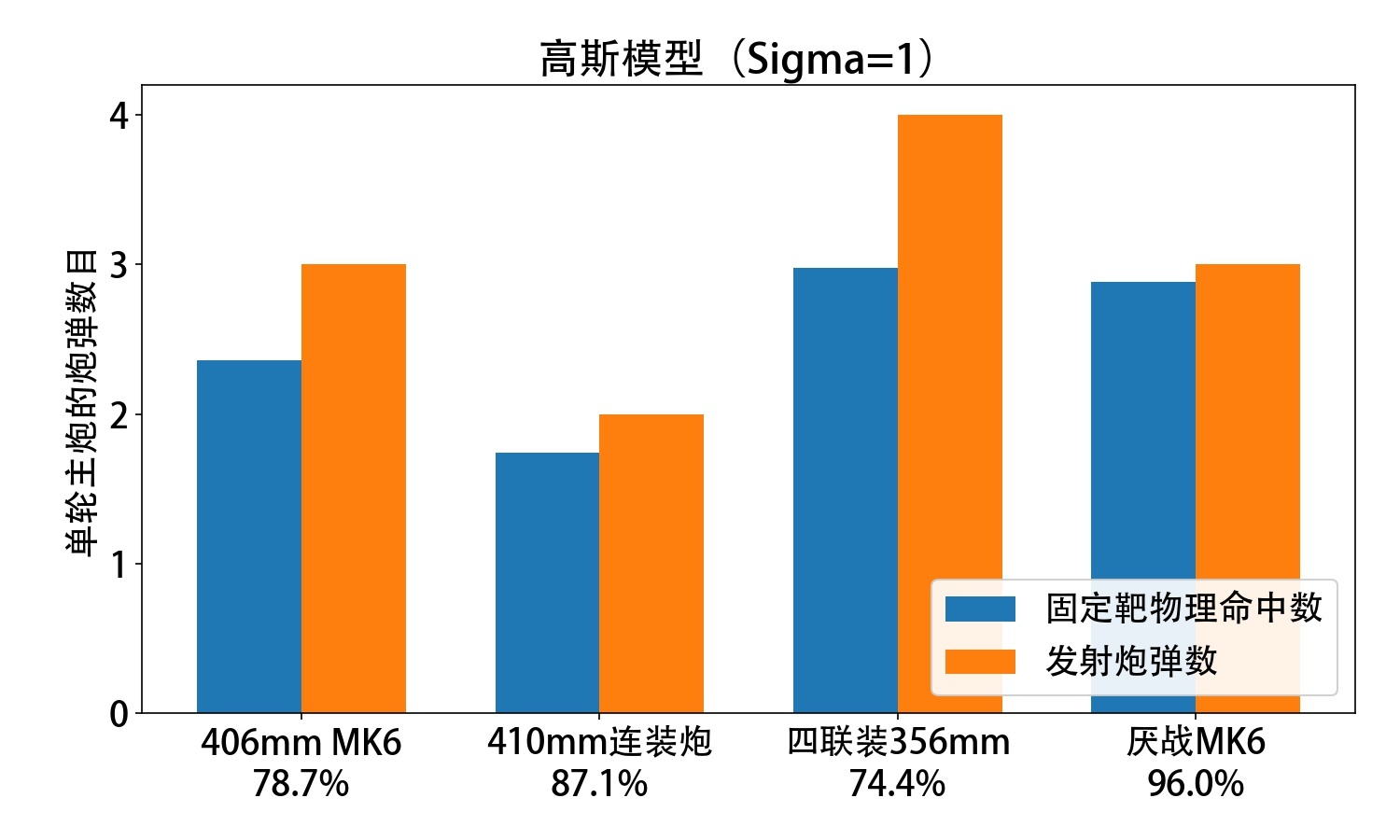
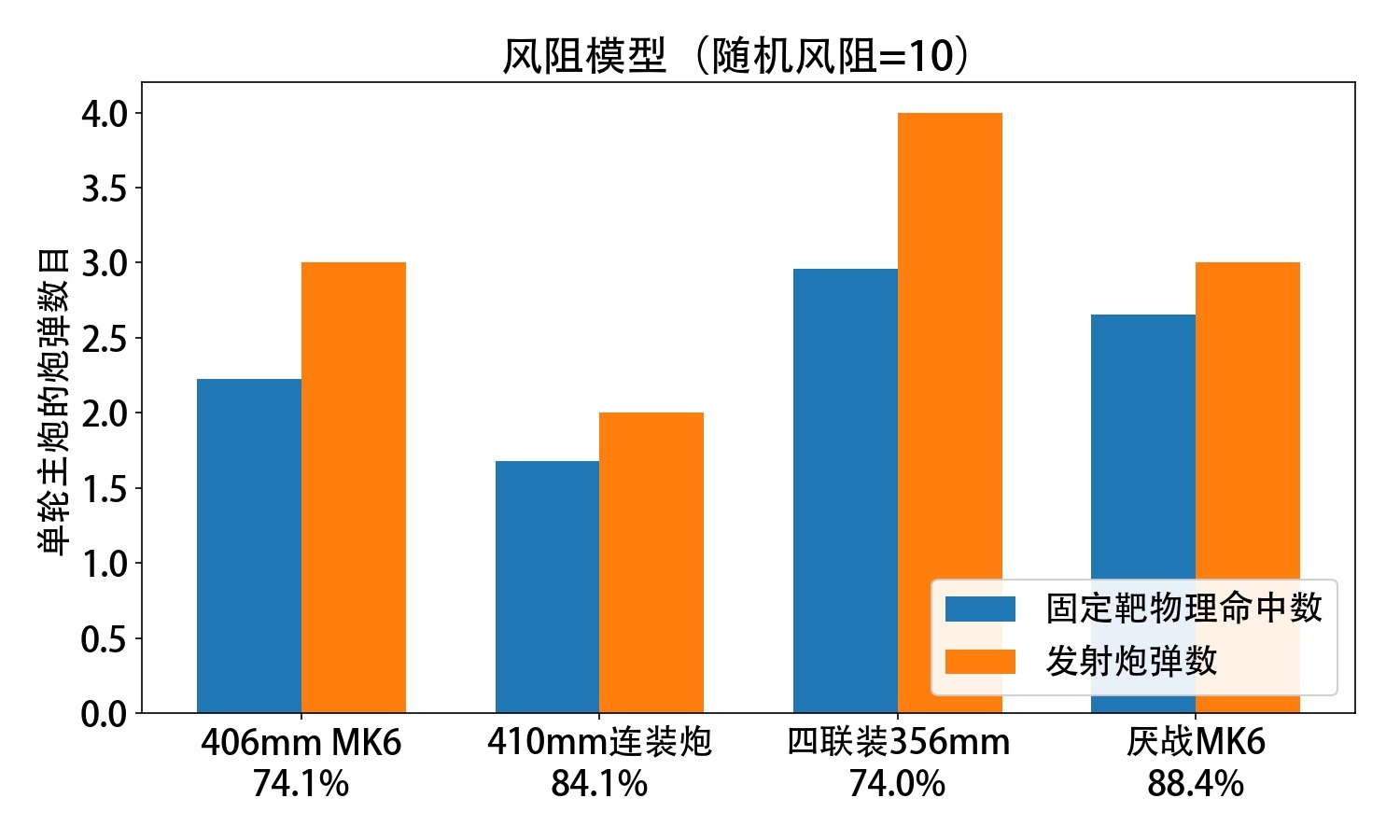
四种主炮单轮平均命中数(蓝色)和单轮发射炮弹数（橙色）如下面的柱状图所示，四种主炮各自的命中率也各做了标识：
| 高斯模型 | 风阻模型 |
|---|---|
|
|
总体而言，高斯模型中，MK6平均每轮可以命中~2.3发，410平均每轮可以命中~1.7发，这和实战还算接近——MK6单轮打固定靶中两炮很容易，三炮全中似乎比较困难；410每轮两炮都中的概率很高，只有脸比较黑的时候才只中一发。厌战改可以将MK6的命中率从78%提高到96%，这对厌战打固定靶的输出提升相当明显。
风阻模型的命中率比高斯模型略低一些，其中MK6、410的命中率（74%，84%）跟小圣的数据比较接近（72%，83%），如果小圣的数据是实战结论的话，那可以说是符合的很好了。另外，新模型中厌战改搭配MK6的命中率就没有96%这么恐怖了（其实我也不是很信高斯模型中96%这个数），新的88.4%的命中率相较于不减散布（74.1%）提升了1.2倍，相当于厌战改减的5点散布带来了20%主炮炮击的增伤。高斯模型给出的结论是22%，其实差的不是很多。
实战中，我们有可能看到这样的情况（据作者舰队的一位不愿透露姓名的老干部）：
那个，反正我13-4 boss战没上过
鲨，所以并不知道鲨是什么样的，而且我13-4打得也不是很多，所以欢迎读者实测反馈。
减散布对主炮命中数的提升
接下来，我们仍然对三种主炮进行测试，探究这一模型下主炮命中数提升率和散布减少量的关系。 这里，散布的减少量取以下数列：a_n = {0, 0.2, 0.4, …, 8.0} 。我们把每个散布减少量a_i带入到各个主炮当中，计算给定a_i下，10000轮主炮射击的单轮平均命中数H_i，并与散布不减少时(H_0)进行比较。
# 定义三个数组，记录三种主炮各自命中率
us_mk6_curve = np.array([])
jp_410_curve = np.array([])
uk_356_curve = np.array([])
# 散布空间(a_n)
disp_space = np.arange(0, 8.2, 0.2)
for neg_disp in disp_space:
tmp_mk6 = Gun(name = '406mm_mk6', shell_num = 3, xz_shift = 19*(22-neg_disp)/22, dispersion = 22-neg_disp)
us_mk6_curve = np.append(us_mk6_curve, tmp_mk6.center_hit_per_round(10000, norm = False))
tmp_410 = Gun(name = '410mm_twin', shell_num = 2, xz_shift = 16*(20-neg_disp)/20, dispersion = 20-neg_disp)
jp_410_curve = np.append(jp_410_curve, tmp_410.center_hit_per_round(10000, norm = False))
tmp_356 = Gun(name = '356mm_quad', shell_num = 4, xz_shift = 19*(25-neg_disp)/25, dispersion = 25-neg_disp)
uk_356_curve = np.append(uk_356_curve, tmp_356.center_hit_per_round(10000, norm = False))
# 误差：取二项分布误差 sqrt(Np(1-p))/N
us_mk6_err = np.sqrt(us_mk6_curve/3. * (1 - us_mk6_curve/3.) / 10000)
jp_410_err = np.sqrt(jp_410_curve/2. * (1 - jp_410_curve/2.) / 10000)
uk_356_err = np.sqrt(uk_356_curve/4. * (1 - uk_356_curve/4.) / 10000)
# 开始绘图
plt.figure(figsize = (8,6))
ax = plt.gca()
plt.errorbar(disp_space, us_mk6_curve/us_mk6_curve[0], yerr = (us_mk6_err**2+us_mk6_err[0]**2)**0.5,
color = 'b', marker = 's', capsize = 5, label = '406mm MK6')
plt.errorbar(disp_space, jp_410_curve/jp_410_curve[0], yerr = (jp_410_err**2+jp_410_err[0]**2)**0.5,
color = 'r', marker = '>', capsize = 5, label = '410mm连装炮')
plt.errorbar(disp_space, uk_356_curve/uk_356_curve[0], yerr = (uk_356_err**2+uk_356_err[0]**2)**0.5,
color = 'g', marker = 'o', capsize = 5, label = '356mm四连装')
# 添加特定点：乔五、复读机、厌战
plt.text(5, 1.30, '厌战改', color= 'k', ha ='center', va='center', fontsize = 16)
plt.axvline(5, 0.85, 0.90, color = 'k')
plt.text(2, 1.30, '乔五\n或 复读机', color= 'k', ha ='center', va='center', fontsize = 16)
plt.axvline(2, 0.82, 0.87, color = 'k')
plt.text(4, 1.28, '乔五+复读机', color= 'k', ha ='center', va='center', fontsize = 16)
plt.axvline(4, 0.79, 0.84, color = 'k')
plt.legend(framealpha = 0.6, loc = 4,
ncol = 1, handletextpad = 0.5, columnspacing = 0.2)
ax.set(xlim = (0, 8), ylim = (1.0, 1.32),
# title = '高斯模型 （Sigma=1）',
xlabel = '散布降低值', ylabel = '固定靶单轮主炮命中数增幅')
ax.set_yticks([1.0, 1.1, 1.2, 1.3])
ax.set_yticklabels(['0%', '10%', '20%', '30%'])
plt.tight_layout()
# plt.savefig('disp_散布降低收益.jpg', dpi = 150)
三门主炮的单轮命中数增幅与散布减少量的关系如下图所示，图里面的误差棒通过二项分布的标准差进行计算：
| 高斯模型 | 风阻模型 |
|---|---|
|
|
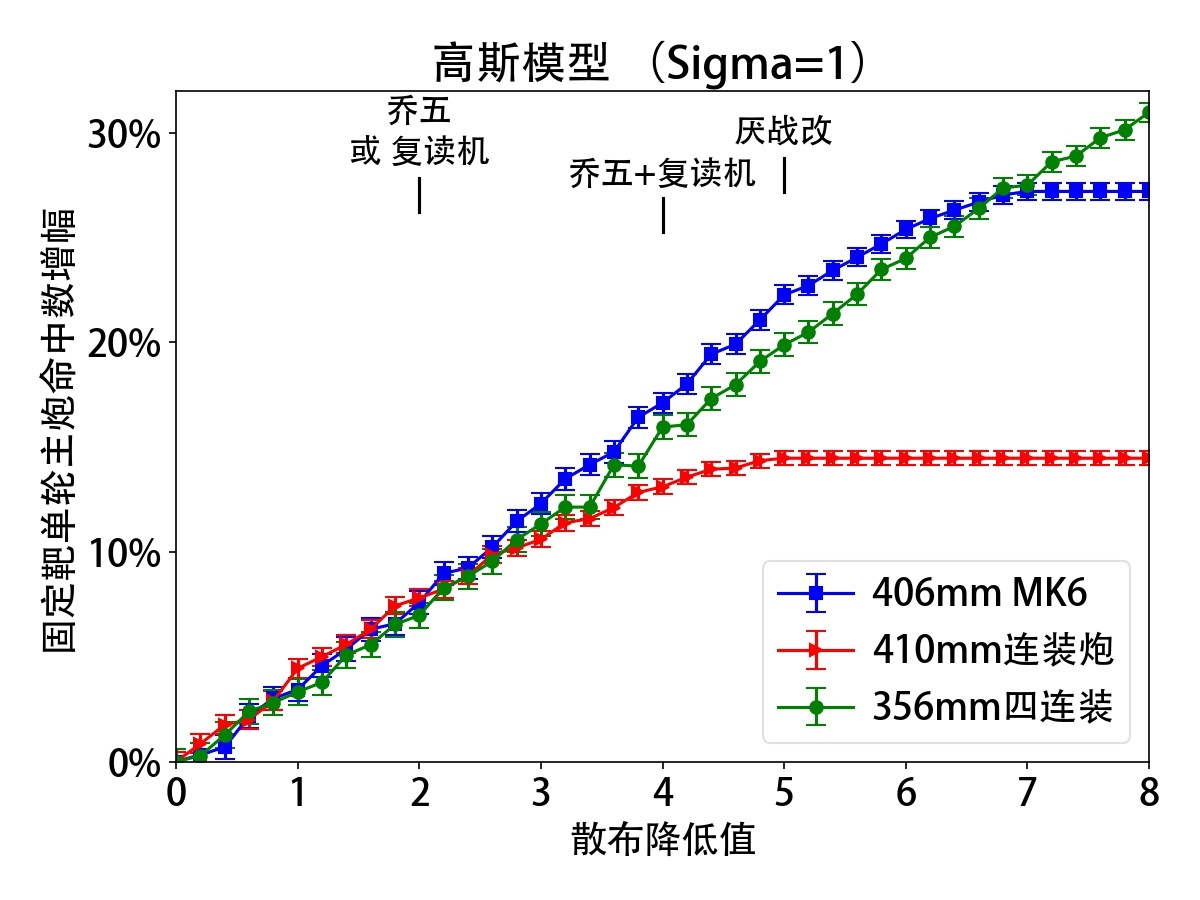
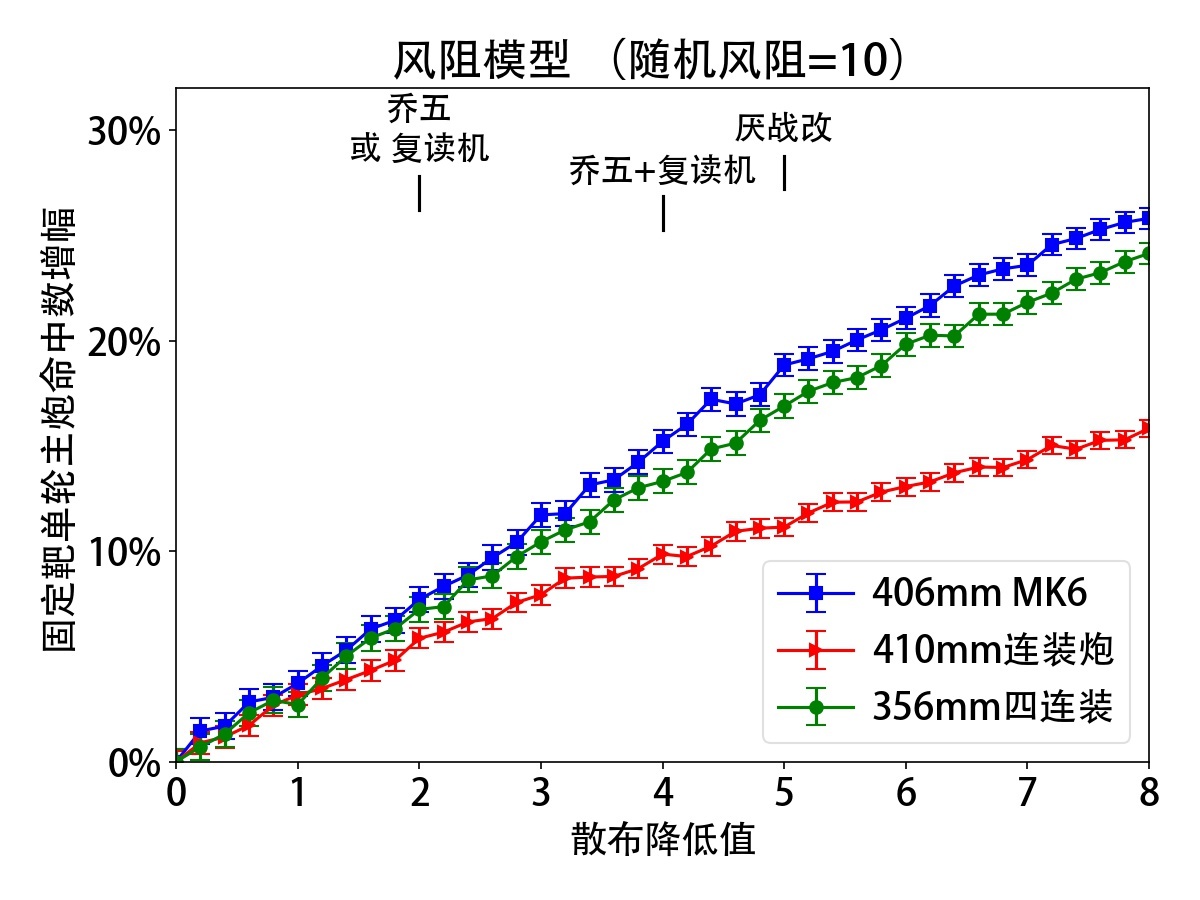
1. 高斯模型： 可以看到，在散布减0~3之间时，三种主炮的命中数提升幅度差别不大，差不多每减1点散布，主炮命中数提升4%。换句话说，对于常见主炮而言，比起空一个装备位置，98式复读机大致可以提高8%的主炮命中数。至于具体相当于提高多少输出，还需要考虑这个装备对炮击面板的影响，以及主炮输出占总输出的比例，这超过了这篇文章的考虑范围。有兴趣的读者可以算一算。
在散布减少3以上时，率先掉队的是410，因为这个炮本身的面板散布就是最小的。减少散布超过4点后，410的两发炮弹都能准确落到15格的物理命中范围内，这时再减散布就没有额外收益了。所以，最好不要给厌战改带410，这对主炮物理命中提升幅度几乎要比MK6小10%。当然，这里不讨论低难图伤害溢出的情形。
由于四联356的面板散布很大，所以在目前可以搭配到的减面板散布的范围内（0~7），给大哥炮减散布都是正收益，而且这个收益的线性很不错。
MK6的线性收益范围大概是0~6，所以厌战改带MK6收益很高。厌战改改在主炮散布减5点并使用MK6时，对固定靶的物理命中期望为2.87发/轮，相对于没有散布降低时提高了22%的物理命中率。带上MK6+98式复读机后，厌战改基本可以做到打固定靶每发必中，但是98式复读机本身的收益是不如黑弹/
白弹的。利用炮击伤害公式计算，对于600炮击值的战列舰而言，黑弹所带来的主炮伤害提升大约为14.4%，而98式复读机算散布收益为8%，则总主炮伤害提升大约是12.9%，这与目前的一些实战结论（如九八式延迟射击装置13-4道中对比超重弹弹链的收益测试）符合得比较不错。
2. 风阻模型： 在目前能搭配出来的减散布范围内（厌战改+98式复读机，减7点），三门炮弹数不同的主炮都有线性的收益规律，而高斯模型中的阈值没有出现。这点说实话我不知道跟实战符合的怎么样，总感觉应该有个阈值才对。这种现象可能是新模型取的风阻偏移比较大（10点）引起的，如果是6~8点，似乎我们就会在这张图的范围里看到收益变差的趋势了。
综合两种模型给出的不同的收益曲线，我们应该可以得出一些普适的基本结论（推论）：
②无论哪种模型，绝大多数情况下，98式复读机对主炮炮击伤害的提升都不如黑弹。
从面板上看，黑弹比98式复读机多了38点炮击，然后主炮暴击率+8%相当于4%主炮增伤（暴击伤害是150%，有特技的除外），而复读机减散布的收益大概是<8%的。所以除非一艘100%主炮输出（没弹幕没副炮）的战列舰炮击能撑到38/4% - 100 = 850，还是不要带复读机了。当然复读机属于减少方差的设备，觉得自己带黑弹也不存在暴击的非洲老弟们可以试试。
结语
在这篇建模讨论中，我们根据主炮设备的面板数值，假设了两种跨射炮弹的散布模型，一种为椭圆高斯分布模型，一种为风阻模型。依照这两种模型，我们用蒙特卡洛的方法，计算了主流主炮MK6和410的命中率，计算结果与实战均较为接近。在两种散布模型下，散布减少量较低时，我们都得到了【主炮命中数目增幅】与【散布减少量】之间的线性关系，每减少1点散布约带来了4%的主炮命中数目增幅。经过计算，厌战改的技能减5点散布，带来的是对固定靶的~20%主炮命中率增幅。同时，对于绝大部分情况，98式复读机对于主炮输出的提升应当不如黑弹。
最后的随后，我还是要强调，实践是检验真理的唯一标准，这里的两个模型均不代表游戏的真正机制，所以至少有一个是错的，而且很可能两个都是错的。模型能做到的，也就是大致让我们对散布模型有点数，肯定解决不了全部的问题。如果这个新模型看起来能经得起更多的检验的话，我会进一步考虑如何把日常战斗中的真实情况纳入考虑（敌舰的移动、分布对物理命中数的影响），进行进一步的建模和统计。这次就先讨论这么多，欢迎读者的讨论、补充和实战的检验。
另外据齿轮大佬指出（如果我理解正确了的话），你游真正的散布模型可能是以射击中心做一个正方形，边长是XZ偏移*2（如果命中范围还是半径15的圆），然后炮弹落点在这里面均匀随机分布。这样算出来MK6的命中率不到50%，感觉很是奇怪，所以在这里我依然坚持原来的这两种建模。欢迎各位大佬继续批评指正，写这篇文章时确实学习了不少有意思的东西。
沪公网安备 31011002002714 号